题目描述

A mysterious cubic alien ship has appeared in the sky over Toronto! In this problem, Toronto is a plane in three-dimensional space that is parallel to the xz plane at $y = -3$ km. The alien ship is a solid cube with side length 1 km, centered at $(0 \text{ km}, 0 \text{ km}, 0 \text{ km})$, with its eight corners at $(\pm 0.5 \text{ km}, \pm 0.5 \text{ km}, \pm 0.5 \text{ km})$. The ship is casting an ominous shadow onto the plane; formally, the shadow is the orthogonal projection of the cube onto the plane. (We consider the sun to be a point infinitely far above the Toronto plane along the y-axis.)

The military is willing to tolerate the ship as long as the aliens meet their bureaucratic demand: the shadow must cover an area of the plane that is acceptably close to $\mathbf A \text{ km}^2$ (see the Output section for a precise definition). They have hired you, a geometric linguistics expert, to convey this demand to the aliens. In your communications so far, you have learned that the ship cannot change size, and the center of the ship cannot move, but the ship is able to rotate arbitrarily in place.

Please find a way that the aliens can rotate the ship so that the shadow's area is close to $\mathbf A$. Express your rotation using three points: the centers of any three non-pairwise-opposing faces.

输入格式

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow; each consists of one line with a rational $\mathbf{A}$, the desired area of the shadow, in $\mathrm{km}^{2}$, with exactly six digits after the decimal point.

It is guaranteed that there is always a way to rotate the ship in the desired manner for the values of $\mathbf{A}$ allowed in this problem.

输出格式

For each test case, first output one line containing Case #x:, where $x$ is the test case number (starting from 1). Then, output three more lines with three rational values each: the $x, y$, and $z$ coordinates of one of your three provided face-centers, as described above. You are welcome to use decimal (e.g., 0.000123456) or scientific notation (e.g., 1.23456e-4).

Your answer will be considered correct if and only if all of the following are true:

1. The distance (in $\mathrm{km}$ ) from each point to the origin must be between $0.5-10^{-6}$ and $0.5+10^{-6}$, inclusive.
2. The angles (in radians) between segments connecting the origin to each point must be between $\pi / 2-10^{-6}$ and $\pi / 2+10^{-6}$, inclusive.
3. The area of the shadow (in $\mathrm{km}^{2}$ ), computed by projecting all 8 vertices onto the $y=-3$ plane and finding the area of the convex hull of those projected points, must be between $\mathbf{A}-10^{-6}$ and $\mathbf{A}+$ $10^{-6}$, inclusive. We will compute the vertices as $+/-\mathbf{p}_{1}+/-\mathbf{p}_{2}+/-\mathbf{p}_{3}$ (that is, for each $\mathbf{p}_{i}$ we add either $\mathbf{p}_{i}$ or $-\mathbf{p}_{i}$ to the total using vector addition), where $\mathbf{p}_{1}, \mathbf{p}_{2}$, and $\mathbf{p}_{3}$ are the face-centers that you provide.

Please note that you might need to output more than 6 digits after the decimal point to safely pass the checks mentioned above. If there are multiple acceptable answers, you may output any one of them.

2
1.000000
1.414213

Case #1:
0.5 0 0
0 0.5 0
0 0 0.5
Case #2:
0.3535533905932738 0.3535533905932738 0
-0.3535533905932738 0.3535533905932738 0
0 0 0.5

提示

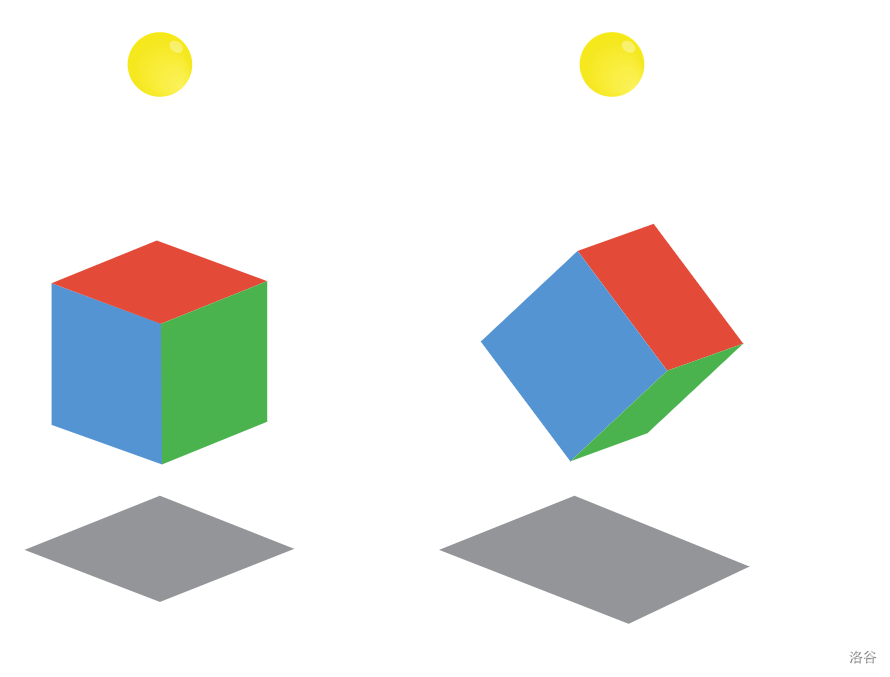
In Sample Case #1, there is no need to rotate the cube at all; with two of its faces already parallel to the plane, the cube is already casting a shadow that is a square with side length $1$.

In Sample Case #2, one possible solution is to tell the aliens to give the cube a $45$ degree turn around the $x = y = 0$ line, creating a shadow that is a rectangle with dimensions of $1$ and $\sqrt 2$.

The following rough image shows the cubes and shadows for Sample Cases #1 and #2. The sun is shown for clarity, but remember that it is actually a point infinitely far away along the y-axis.

Limits

• $1 \leqslant \mathrm{T} \leqslant 100$.

Test set 1 (Visible)

• $1.000000 \leqslant \mathrm{A} \leqslant 1.414213$

Test set 2 (Hidden)

• $1.000000 \leqslant \mathrm{A} \leqslant 1.732050$