题目描述

The Code Jam team has just purchased an orchard that is a two-dimensional matrix of cells of unprepared soil, with $1000$ rows and $1000$ columns. We plan to use this orchard to grow a variety of trees — AVL, binary, red-black, splay, and so on — so we need to prepare some of the cells by digging holes:

• In order to have enough trees to use for each year's tree problems, we need there to be at least $A$ prepared cells.
• In order to care for our trees properly, the set of all prepared cells must form a single grid-aligned rectangle in which every cell within the rectangle is prepared.

Note that the above also implies that none of the cells outside of that rectangle can be prepared. We want the orchard to look tidy!

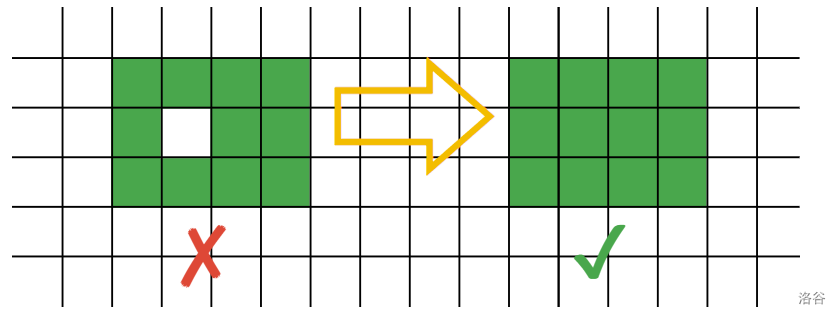
For example, when $\mathbf A=11$, although the eleven prepared cells in the left figure below form a $3 \times 4$ rectangle (that is, with $3$ rows and $4$ columns), the cell in the center of the rectangle is not prepared. As a result, we have not yet completed preparing our orchard, since not every cell of the $3 \times 4$ rectangle is prepared. However, after just preparing the center cell, the rectangle of size at least $11$ is fully filled, and the orchard is ready.

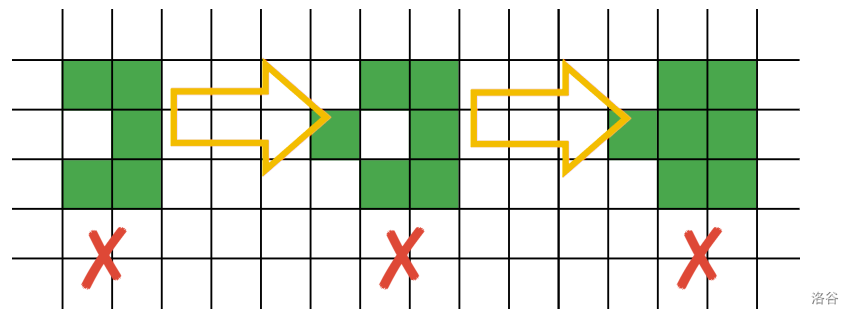
See below for another example. In this case, $\mathbf{A}=6$. Note that the middle figure prepares a cell outside the $3\times 2$ rectangle, so although the rightmost figure prepares a rectangle of size $6$, the entire set of the prepared cells does not form a rectangle (due to the extra cell on the left). As a result, the orchard is not ready.

Digging is hard work for humans, so we have borrowed the Go gopher from the Google Go team and trained it to help us out by preparing cells. We can deploy the gopher by giving it the coordinates of a target cell in the matrix that is not along any of the borders of the matrix. However, we have not yet perfected the gopher's training, so it will choose a cell uniformly at (pseudo-)random from the $3\times 3$ block of nine cells centered on the target cell, and then prepare the cell it has chosen. (If it chooses a cell that was already prepared, it will uselessly prepare it again.)

We can only deploy the gopher up to $1000$ times before it gets too tired to keep digging, so we need your help in figuring out how to deploy it strategically. When you deploy the gopher, you will be told which cell the gopher actually prepared, and you can take this information into account before deploying it again, if needed. Note that you do not have to declare the dimensions or location of a rectangle in advance.

Interactive Protocol

This problem is interactive, which means that the concepts of input and output are different than in standard Code Jam problems. You will interact with a separate process that both provides you with information and evaluates your responses. All information comes into your program via standard input; anything that you need to communicate should be sent via standard output. Remember that many programming languages buffer the output by default, so make sure your output actually goes out (for instance, by flushing the buffer) before blocking to wait for a response. See the FAQ for an explanation of what it means to flush the buffer. Anything your program sends through standard error is ignored, but it might consume some memory and be counted against your memory limit, so do not overflow it. To help you debug, a local testing tool script (in Python) is provided at the very end of the problem statement. In addition, sample solutions to a previous Code Jam interactive problem (in all of our supported languages) are provided in the analysis for Number Guessing.

Initially, your program should read a single line containing a single integer $\mathbf T$ indicating the number of test cases. Then, you need to process $\mathbf T$ test cases.

For each test case, your program will read a single line containing a single integer $\mathbf A$ indicating the minimum required prepared rectangular area. Then, your program will process up to $1000$ exchanges with our judge.

For each exchange, your program needs to use standard output to send a single line containing two integers $I$ and $J$: the row and column number you want to deploy the gopher to. The two integers must be between $2$ and $999$, and written in base-10 without leading zeroes. If your output format is wrong (e.g., out of bounds values), your program will fail, and the judge will send you a single line with $-1 -1$ which signals that your test has failed, and it will not send anything to your input stream after that. Otherwise, in response to your deployment, the judge will print a single line containing two integers $I'$ and $J'$ to your input stream, which your program must read through standard input.

If the last deployment caused the set of prepared cells to be a rectangle of area at least $\mathbf A$, you will get $I' = J' = 0$, signaling the end of the test case. Otherwise, $I'$ and $J'$ are the row and column numbers of the cell that was actually prepared by the gopher, with $\text{abs}(I'-I) \leq 1$ and $\text{abs}(J'-J) \leq 1$. Then, you can start another exchange.

If your program gets something wrong (e.g. wrong output format, or out-of-bounds values), as mentioned above, the judge will send $I' = J' = -1$, and stop sending output to your input stream afterwards. If your program continues to wait for the judge after reading in $I' = J' = -1$, your program will time out, resulting in a Time Limit Exceeded error. Notice that it is your responsibility to have your program exit in time to receive the appropriate verdict (Wrong Answer, Runtime Error, etc.) instead of a Time Limit Exceeded error. As usual, if the total time or memory is exceeded, or your program gets a runtime error, you will receive the appropriate verdict.

If the test case is solved within $1000$ deployments, you will receive the $I' = J' = 0$ message from the judge, as mentioned above, and then continue to solve the next test case. After $1000$ exchanges, if the test case is not solved, the judge will send the $I' = J' = -1$ message, and stop sending output to your input stream after.

You should not send additional information to the judge after solving all test cases. In other words, if your program keeps printing to standard output after receiving $I' = J' = 0$ message from the judge for the last test case, you will receive a Wrong Answer judgment.

Please be advised that for a given test case, the cells that the gopher will pick from each $3 \times 3$ block are (pseudo-)random and independent of each other, but they are determined using the same seed each time for the same test case, so a solution that gives an incorrect result for a test case will do so consistently across all attempts for the same test case. We have also set different seeds for different test cases.

输入格式

See Interactive Protocol.

输出格式

See Interactive Protocol.

提示

Sample Interaction

  t = readline_int()         // reads 2 into t
  a = readline_int()         // reads 3 into a
  printline 10 10 to stdout  // sends out cell 10 10 to prepare
  flush stdout
  x, y = readline_two_int()  // reads 10 11, since cell 10 11 is prepared
  printline 10 10 to stdout  // sends out cell 10 10 again to prepare
  flush stdout
  x, y = readline_two_int()  // reads 10 10, since cell 10 10 is prepared
  printline 10 12 to stdout  // sends out cell 10 12 to prepare
  flush stdout
  x, y = readline_two_int()  // reads 10 11, since cell 10 11 is prepared again
  printline 10 10 to stdout  // sends out cell 10 10 to prepare
  flush stdout
  x, y = readline_two_int()  // reads 11 10, since cell 11 10 is prepared
  printline 11 10 to stdout  // sends out cell 11 10 to prepare
  flush stdout
  x, y = readline_two_int()  // reads 0 0; since cell 11 11 is prepared, a rectangle of size 4

The pseudocode above is the first half of a sample interaction for one test set. Suppose there are only two test cases in this test set. The pseudocode first reads the number of test cases into an integer $t$. Then the first test case begins. For the first test case, suppose $\mathbf A$ is $3$ (although, in the real test sets, $\mathbf A$ is always either $20$ or $200$). The pseudocode first reads the value of $\mathbf A$ into an integer $a$, and outputs $10 \ 10$ the location of the cell to prepare. By (pseudo-)random choice, the cell at location $10 \ 11$ is prepared, so the code reads $10 \ 11$ in response. Next, the code outputs cell $10 \ 10$ again for preparation, and the gopher prepares $10 \ 10$ this time. The code subsequently sends $10 \ 12$ with the goal of finishing preparing a rectangle of size $3$, but only gets cell $10 \ 11$ prepared again. $10 \ 10$ is then sent out, and this time $11 \ 10$ is prepared. Notice that although the prepared area is of size $3$, a rectangle has not been formed, so the preparation goes on. In the end, the pseudocode decides to try out cell $11 \ 10$, and $0 \ 0$ is sent back, which implies that cell $11 \ 11$ has been prepared, completing a rectangle (or square, rather) or size $4$. As a result, the first test case is successfully solved.

  a = readline_int()         // reads 3 into a
  printline 10 10 to stdout  // sends out cell 10 10 to prepare
  x, y = readline_two_int()  // does not flush stdout; hangs on the judge

Now the pseudocode is ready for the second test case. It again first reads an integer $a = 3$ and decides to send cell $10\ 10$ to prepare. However, this time, the code forgets to flush the stdout buffer! As a result, $10\ 10$ is buffered and not sent to the judge. Both the judge and the code wait on each other, leading to a deadlock and eventually a Time Limit Exceeded error.

  a = readline_int()         // reads 3 into a
  printline 1 1 to stdout    // sends out cell 1 1 to prepare
  x, y = readline_two_int()  // reads -1 -1, since 1 is outside the range [2, 999]
  printline 10 10 to stdout  // sends a cell location anyway
  x, y = readline_two_int()  // hangs since the judge stops sending info to stdin

The code above is another example. Suppose for the second test case, the code remembers to flush the output buffer, but sends out cell $1 \ 1$ to prepare. Remember that the row and column of the chosen cell must both be in the range $[2, 999]$, so $1 \ 1$ is illegal! As a result, the judge sends back $-1 \ -1$. However, after reading $-1 \ -1$ into $x$ and $y$, the code proceeds to send another cell location to the judge, and wait. Since there is nothing in the input stream (the judge has stopped sending info), the code hangs and will eventually receive a Time Limit Exceeded error.

Note that if the code in the example above exits immediately after reading $-1 \ -1$, it will receive a Wrong Answer instead:

  a = readline_int()         // reads 3 into a
  printline 1 1 to stdout    // sends out cell 1 1 to prepare
  x, y = readline_two_int()  // reads -1 -1, since 1 is outside the range [2, 999]
  exit                       // receives a Wrong Answer judgment

You can use this testing tool to test locally or on our platform. To test locally, you will need to run the tool in parallel with your code; you can use our interactive runner for that. For more information, read the instructions in comments in that file.

Instructions for the testing tool are included in comments within the tool. We encourage you to add your own test cases. Please be advised that although the testing tool is intended to simulate the judging system, it is NOT the real judging system and might behave differently.

Limits

$1 \leqslant T \leqslant 20$.

Test set 1 (10 Pts, Visible)

• $A=20$.
• Time limit (for the entire test set): 20 seconds.

Test set 2 (20 Pts, Hidden)

• $A=200$.
• Time limit (for the entire test set): 60 seconds.