#P12747. [POI 2016 R3] 巡游 Parade
[POI 2016 R3] 巡游 Parade
题目背景
翻译来自于 LibreOJ。
题目描述
题目译自 XXIII Olimpiada Informatyczna — III etap Parada
每年春天,拜托城都会举办盛大的拜托尼亚春季巡游,迎接新季的到来。今年,国王 Bajtazar XVI 亲临现场,为巡游增添光彩。拜托城的路网由 个路口通过 条双向街道连接而成,确保从任一路口可到达其他任意路口。
巡游的具体路线尚未确定,但已知它将从某路口出发,沿若干街道行进,最终在另一路口结束。为避免单调,巡游路线每条街道至多经过一次。
为确保巡游参与者的安全,需在巡游经过的路口(包括起点和终点)处,对未被巡游使用的街道入口设置路障。请计算最多可能需要多少路障。
输入格式
第一行包含一个整数 ,表示拜托城的路口数量。路口编号为 至 。
接下来的 行描述拜托城的路网,每行包含两个整数 ,表示路口 和 间存在一条双向街道。
输出格式
输出一行,包含一个整数,表示保障巡游安全最多可能需要的路障数量。
8
1 2
2 3
4 2
5 2
6 5
5 7
7 8
5
提示
样例 1 解释
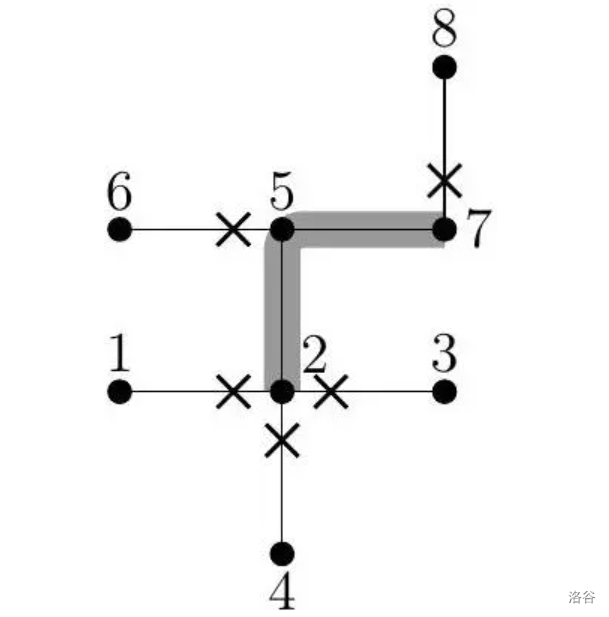
若巡游从路口 出发,至路口 结束,需设置 处路障(路口 的 个入口各一处,路口 和 各一处)。
附加样例
- ,路网为路径。
- ,路网为星形。
- ,随机样例,第 条街道()连接路口 与某编号更小的路口。
详细子任务附加限制及分值如下表所示。
| 子任务 | 附加限制 | 分值 |
|---|---|---|
