题目背景

试题来源：https://koi.or.kr/archives/。中文翻译做了少量本土化修改。

按照署名—非商业性使用—相同方式共享 4.0 协议国际版进行授权。

题目描述

在坐标平面上有 $N$ 个红色点和 $M$ 个蓝色点。给定自然数 $W$ 和 $H$。

第 $i$ 个 ($1 \leq i \leq N$) 红色点的坐标是 $(r_{xi}, r_{yi})$，第 $j$ 个 ($1 \leq j \leq M$) 蓝色点的坐标是 $(b_{xj}, b_{yj})$。

所有点的坐标都是不同的。

我们需要放置一个宽度为 $W$，高度为 $H$ 的矩形，该矩形的边与坐标轴平行，并且它的四个顶点是整数坐标。我们希望最大化矩形内包含的红色点与蓝色点数量之差。

矩形包含点的条件是：如果矩形的左下角坐标为 $(a, b)$，且点的坐标为 $(x, y)$，那么该点包含在矩形内当且仅当满足 $a \leq x \leq a+W$ 且 $b \leq y \leq b+H$。

我们要求得这个差值的最大值，并找到符合这个最大差值的矩形位置。

下图展示了在平面上有 3 个红色点和 4 个蓝色点的情况。为了说明问题，红色点用圆圈表示，蓝色点用三角形表示。

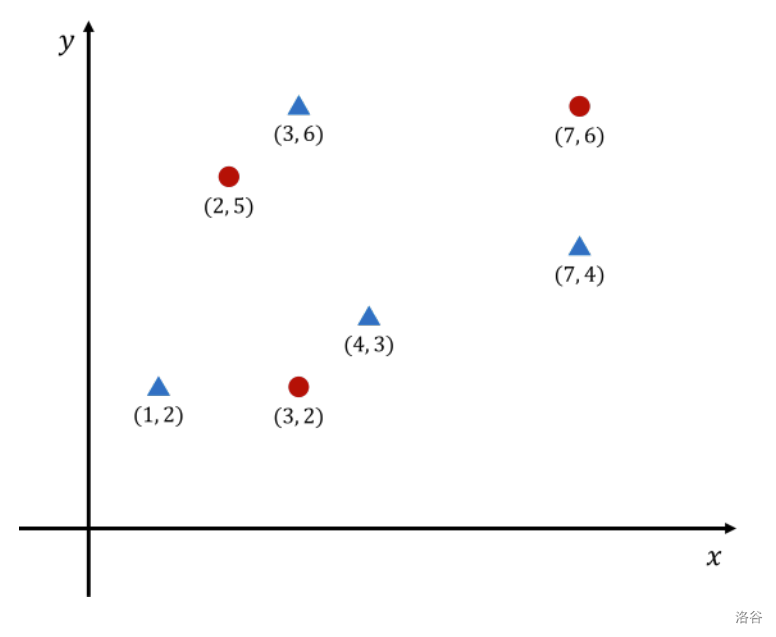
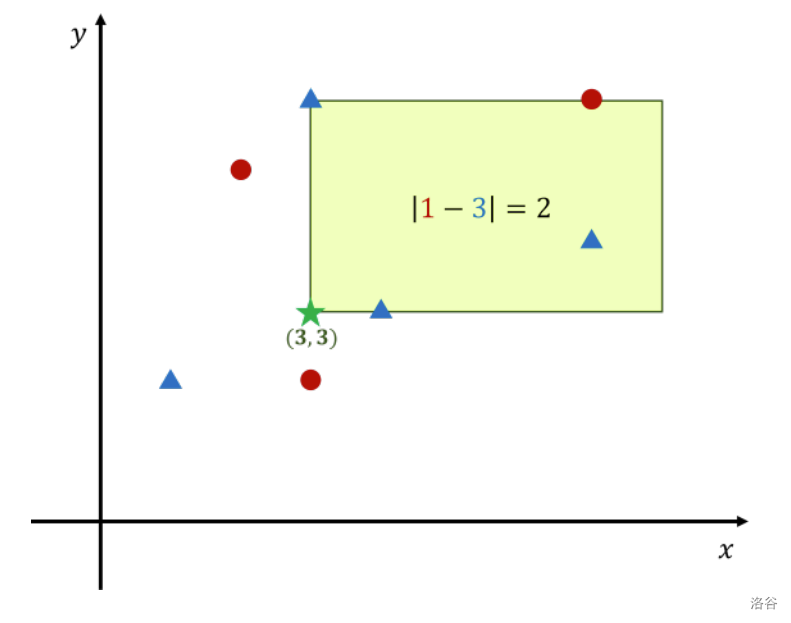
假设 $W = 5$，$H = 3$，那么如果将矩形的左下角放在 $(3, 3)$，矩形内包含 1 个红色点和 3 个蓝色点，这时点的数量差为 2。无论矩形放置在哪里，点的数量差都不会大于 3，因此答案是 2。

输入格式

第一行给出整数 $N$ 和 $M$，以及矩形的宽度 $W$ 和高度 $H$。

接下来的 $N$ 行，每行包含一个红色点的坐标 $(r_{xi}, r_{yi})$。

接下来的 $M$ 行，每行包含一个蓝色点的坐标 $(b_{xj}, b_{yj})$。

输出格式

输出一个整数，表示最大点数差值。然后输出矩形左下角的坐标 $(a, b)$。

如果答案有多个，输出任意一个即可。

3 4 5 3
3 2
2 5
7 6
1 2
4 3
3 6
7 4

2
3 3

3 3 4 4
1 1
2 2
3 3
1 3
3 1
4 4

2
-2 -2

提示

约束条件

• $1 \leq N, M \leq 100\,000$
• $1 \leq W, H \leq 10^9$
• $1 \leq r_{xi}, r_{yi} \leq 10^9$ ($1 \leq i \leq N$)
• $1 \leq b_{xj}, b_{yj} \leq 10^9$ ($1 \leq j \leq M$)

子任务

1. （5 分）$1 \leq N, M, W, H, r_{xi}, r_{yi}, b_{xj}, b_{yj} \leq 50$
2. （11 分）$1 \leq N, M, W, H, r_{xi}, r_{yi}, b_{xj}, b_{yj} \leq 1\,000$
3. （15 分）$1 \leq N, M \leq 100$
4. （9 分）$1 \leq N, M \leq 1\,000$
5. （60 分）无额外约束条件