题目背景

无有因，何果？

题目描述

在题目描述的末尾提供有形式化题意，请注意本题特殊的内存限制。

你被流放在了时间与空间的轮回之中。等待你的，只有无尽岁月的缓慢流淌，与无尽深渊的永恒凝视。不过神打算宽恕你，所以他给了你一个能够重获新生的机会。

现在，「神」拿出了 $n$ 枚黑色棋子和 $m$ 枚白色棋子，以及 $k$ 种不同大小的盒子，第 $i$ 种盒子有 $a_i$ 个。其中，对于 $\forall i \in [1,k-1]$，一个第 $i+1$ 种盒子可以存放任意个第 $i$ 种盒子。这些棋子除颜色外都没有区别，同类的盒子也都没有区别。

然后，你可以随意的把这 $n+m$ 个棋子分配到第 $1$ 种盒子中，棋子不能有剩余，每个第 $1$ 种盒子也不能为空。接下来，仿照第一步，再依次把第 $i$ 种盒子分配到第 $i+1$ 种盒子当中，同样第 $i$ 种盒子不能有剩余，每个第 $i+1$ 种盒子也不能为空。

完成这些操作后，你的面前将存在多个最大规格的盒子，每个最大规格的大盒子内嵌套着若干个次大规格的盒子，每个次大规格的盒子又嵌套着若干个稍小规格盒子，以此类推，直至最小规格的盒子，且盒子里都放置有盒子或棋子。

最后，你需要先随机地选择一个最大规格的盒子，再随机地选择一个其中次大的盒子，以此类推，直到随机摸出一枚棋子，若该棋子是黑色的，那么你就能够被「神」接纳；否则，你将永远待在时间与空间的轮回之中。

当然，你并不想待在这个暗无天日之处。你想知道，你能够被宽恕的最大概率是多少。

由于「神」并不希望你的答案有精度误差，所以你需要输出答案对 $998244353$ 取模的结果。

形式化题意

给你一棵高度为 $k+2$ 的树，从底往上，树的第 $0$ 层（即最底层）有 $n+m$ 个点，其中有 $n$ 个点是黑色的，$m$ 个点是白色的。树的第 $i\in[1,k]$ 层有 $a_i$ 个节点，这些点没有颜色。树的根节点连向每个第 $k$ 层的节点。

你需要构造一种连边方案，满足除最底层节点外，每个节点至少有一个儿子节点。并且使得从树的根节点出发，每次随机地走到该节点的一个儿子节点，一直走到最底层节点为止，停留在黑色节点的概率最大。你需要输出最大概率对 $998244353$ 取模的结果。

输入格式

由于数据过大无法上传，所以你需要用一种特殊方式读入 $a_i$。

第一行 $3$ 个整数 $n,m,k$，表示黑子，白子的数量以及盒子的种类数。

第二行 $3$ 个整数 $a_1,d,x$，表示 $a_1$ 的值以及两个参数，剩下的 $a$ 可以通过以下计算得到：

$$a_i=(a_{i-1}-d)\oplus x$$

特别的，当 $k=0$ 时，你应该忽略掉第二行的内容。

注释：$a \oplus b$ 代表 $a$ 和 $b$ 的按位异或值。

输出格式

一行 $1$ 个整数，表示你能够被宽恕的最大概率对 $998244353$ 取模的结果。

1 2 1
2 0 0

499122177

3 4 3
6 1 1

831870295

提示

这是一份读入数据的示例：

#include <bits/stdc++.h>
using namespace std;
const int N=1e7+5;
int n,m,k,d,x;
int a[N];
int main(){
	cin>>n>>m>>k;
	cin>>a[1]>>d>>x;
	for(int i=2;i<=k;i++){
		a[i]=((a[i-1]-d)^x);
	}
	return 0;
}

该读入示例保证能正确读入数据，但是不保证该示例的内存占用满足全部数据的内存限制。

样例 $1$ 解释

一共只有 $1$ 种盒子，该种盒子有 $2$ 个。
先把 $1$ 颗黑子放入一个盒子中，再把 $2$ 颗白子放入另一个盒子中即可达到最大概率。
答案为 $\frac{1}{2}$，取模后为 $499122177$。

样例 $2$ 解释

一共只有 $3$ 种盒子，每种盒子分别有 $6$ 个，$4$ 个，$2$ 个。
答案为 $\frac{5}{6}$，取模后为 $831870295$。

下图是一种可能的摆放方法，但是并不能使概率最大化。

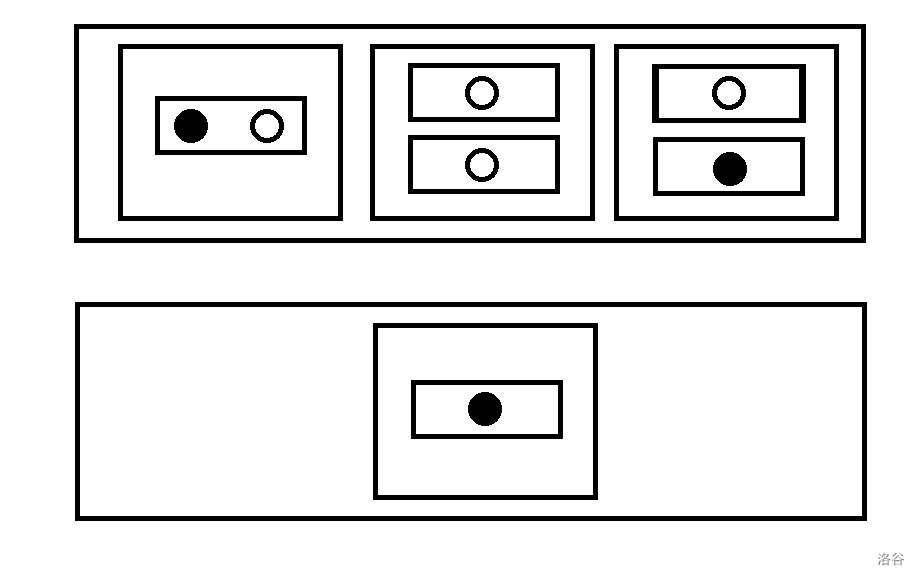
数据范围

对于全部的数据：$0\le n,m\le 10^9$，$0\le x\le d\le 10^9$，$0\le k\le 10^7$，$1\le a_k\le a_{k-1}\le\dots\le a_1\le n+m\le2\times10^9$，详细数据范围见下表。

数据保证答案在模 $998244353$ 下有意义。

Subtask 编号	$n,m$	$k$	特殊限制	分值
#1		$=0$		$5$
#2	$\le 5$	$=1$	$a_1\le5$	$10$
#3			$a_1=2$
#4
#5		$=2$		$15$
#6				$25$
#7			$10$ MB 内存限制

注：默认空间限制是 $512$ MB。