题目描述

Pani Annochka recently got an interview with an IT company. In this interview, she was given a very interesting task:

The girl is given a field divided into squares. That is, each side is $1$. And each square is painted in either white or black.

We say that a chessfield has sizes $n$ and $m$, when it consists of rectangles having $n$ units in height and $m$ units in width. Also, all these rectangles should be painted either white or black. And each white rectangle borders only on black and vice versa --- each black borders only on white.

For example, the following chessboard has sizes $2$ and $3$ (blue is the coordinate axis):

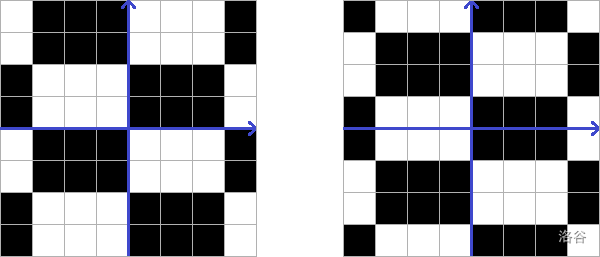
But these are not:

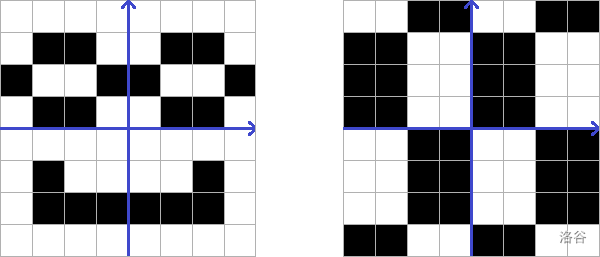
As you may have noticed, there are often a lot of chessfiels with sizes $n$ and $m$. The challenge is to say how many there are. No-no-no, it's too easy.

Annochka also knows $k$ squares on this field and their colors. Pani must find the number of chessfields with sizes $n$ and $m$ such that the squares with the corresponding coordinates have the specified colors. Help her do it!

More formally, you are given $k$ triplets of numbers: $x_i, y_i, c_i$, where ($x_i,y_i$) --- the coordinates of the lower left edge of the square, and $c_i$ is $0$ if this square is to be is painted black, and is $1$ if this square is to be painted white. You need to print the number of different chessfields with sizes $n$ and $m$ that fit under these constraints. Two chessfields are considered different if there is at least one square painted in different colors on these planes.

输入格式

The first line contains four integers $n$, $m$, $k$, $g$ ($1 \leq k \leq 10^5$, $1 \leq n, m \leq 10^9$, $0 \leq g \leq 4$) --- the height of each rectangular, the width of each rectangular, the number of known squares and the number of group.

Each of the next $k$ lines contains three integers $x_i$, $y_i$, $c_i$ ($1 \leq x_i, y_i \leq 10^9, 0 \leq c_i \leq 1$) --- the coordinates and color size. Note that coordinates can be repeated.

输出格式

Print one integer --- the number of different chess planes with sizes $n$ and $m$ that fit the given constraints.

2 2 4 0
1 4 0
2 3 0
3 3 1
4 4 1

1

2 6 2 0
1 2 0
3 2 0

8

提示

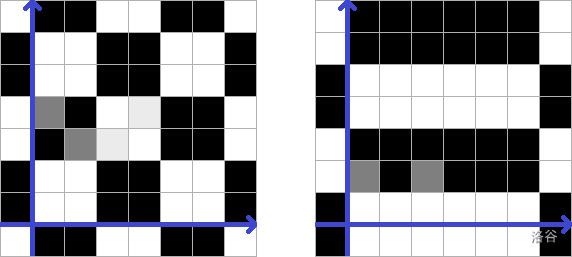
On the left is an image of a single plane that fits the $1$ example limit.

On the right side there is one of the $8$ possible chessfields that satisfy the conditions of the example $2$.

(Blue is the coordinate axis, light gray --- squares, which should be white, dark gray --- squares, which should be black).

• ($17$ points): $1 \leq n, m, x_i, y_i, k \leq 100$;
• ($24$ points): $1 \leq n, m, k \leq 100$;
• ($31$ points): $1 \leq n \cdot m \leq 10^5, 1 \leq k \leq 10^4$;
• ($28$ points): without additional restrictions.