题目描述

Vus the Cossack lives in a skyscraper.

Since he started working as a builder, $n$ customers gave him the task to build $n$ skyscrapers. One of them should be at a distance of one kilometer from the skyscraper of Vus the Cossack, the other should be at a distance of two kilometers, the other should be at a distance of three kilometers and so on. All skyscrapers (including Cossack) must be on the same line, with his skyscraper being the leftmost.

The $i$-th customer wants his skyscraper to be $a_i$ high. However, customers do not care how far their skyscrapers will be from the Vus' skyscraper. Therefore, the Cossack can decide for himself in what order to build other skyscrapers from his skyscraper.

Vus the Cossack wants to make the view from his skyscraper as beautiful as possible. We will assume that the $i$-th floor of a certain skyscraper is visible from the Mustache skyscraper only if there is no other skyscraper between them that will have the $i$-th floor. Vus the Cossack believes that every floor of the $i$-th skyscraper has the beauty of $b_i$. Therefore, he wants the total beauty of all the floors he will see from his skyscraper to be as great as possible.

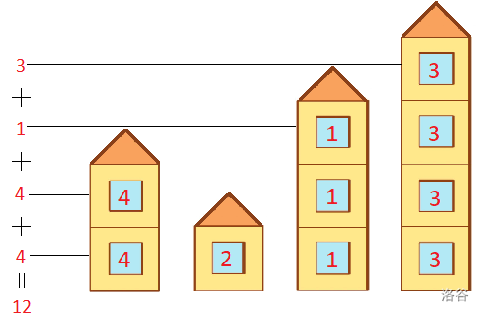
An example for $n$ = 4.

The figure shows an example for $n=4$. At a distance of one kilometer built a two-story skyscraper with the beauty of $4$. Then one-story with the beauty of $2$. Then a three-story with the beauty of $1$. Finally, the latter built a $4$-story skyscraper with a $3$ beauty. From the Vus' skyscraper you can see only both floors of the first skyscraper, the third floor of the third and the fourth floor of the fourth skyscraper. Accordingly, we consider the total beauty of these floors: $4+4+1+3=12$. Note that this may not be the optimal order of construction.

Help him find the maximum possible beauty.

输入格式

The first line contains one integer $n$ ($1 \leq n \leq 10^5$) --- the number of skyscrapers that need to be built.

The second line contains $n$ integers $a_1, a_2, \dots, a_n$ ($1 \leq a_i \leq 10^9$) --- the height of skyscrapers.

The third line contains $n$ integers $b_1, b_2, \dots, b_n$ ($1 \leq b_i \leq 10^9$) --- the beauty of the floors in the skyscrapers.

输出格式

Print one integer --- the maximum possible total beauty.

4
2 1 3 4
4 2 1 3

14

6
1 10 3 9 8 2
8 3 2 4 5 6

51

提示

• ($10$ points) $1 \leq n \leq 10, 1 \leq a_i \leq 10, 1 \leq b_i \leq 10$;
• ($27$ points) $1 \leq n \leq 10^3, 1 \leq a_i \leq 10^3, 1 \leq b_i \leq 10^3$;
• ($25$ points) $1 \leq n \leq 10^3, 1 \leq a_i \leq 10^9, 1 \leq b_i \leq 10^9$;
• ($38$ points) without additional restrictions.