题目描述

A simple polygon is a polygon that is not self-intersecting and does not contain any holes. You are given the $N$ vertices of a simple polygon, $v_1$, $v_2$, $\ldots$, $v_N$, where $v_i = (x_i, y_i)$, and $x_i$ and $y_i$ are the $x$-coordinate and $y$-coordinate of the $i^{\textrm{th}}$ vertex, respectively. The vertices are distinct and given in counterclockwise order (so there is an edge between each pair of consecutive vertices; there is also an edge from $v_N$ back to $v_1$).

The polygon's boundary does not pass through any lattice points (a lattice point is a point where both coordinates are integers). In addition, none of the $x_i$ or $y_i$ values are exactly an integer.

A semi-integer point is a point where exactly one of its coordinates is an integer. Let $\mathcal{P} = \left\{p_1, p_2, \ldots, p_k\right\}$ be all of the semi-integer points that lie on the boundary of the polygon. For each semi-integer point $p_i$ in $\mathcal{P}$, let $n_i$ be the floor of the non-integer coordinate of $p_i$. For a subset $\mathcal{S}$ of $\mathcal{P}$, let $\sigma(\mathcal{S})$ be the sum of the $n_i$ of the points in $\mathcal{S}$ (with $\sigma(\emptyset) = 0$). Does there exist a partition of $\mathcal{P}$ into two subsets $\mathcal{S}_1$ and $\mathcal{S}_2$ so that the $\sigma(\mathcal{S}_1) = \sigma(\mathcal{S}_2)$?

(Two sets $\mathcal{S}_1$ and $\mathcal{S}_2$ are a partition of $\mathcal{P}$ if $\mathcal{P} = \mathcal{S}_1 \cup \mathcal{S}_2$ and $\mathcal{S}_1 \cap \mathcal{S}_2 = \emptyset$. There are no other restrictions on $\mathcal{S}_1$ and $\mathcal{S}_2$ so long as these two conditions hold and $\sigma(\mathcal{S}_1) = \sigma(\mathcal{S}_2)$. In particular, empty sets are allowed, and the semi-integer points in each set do not have to be contiguous around the polygon boundary.)

输入格式

The first line of input contains one integer $N$ ($3 \leq N \leq 500$), the number of vertices of the polygon.

Each of the next $N$ lines contains two space-separated real numbers $x_i$ and $y_i$ ($-500 < x_i, y_i < 500$): the coordinates of the polygon vertices, in counterclockwise order. Each coordinate will have exactly $6$ digits after the decimal point and will not be exactly an integer.

It is guaranteed that the polygon does not self-intersect, that the vertices are distinct, and that the polygon boundary does not pass through any lattice points.

输出格式

If there is no solution, print $-1$ and no further output.

Otherwise, print a single integer $M$ on its own line: the number of semi-integer points in one of the two subsets in a valid partition of $\mathcal{P}$. On the next $M$ lines of output, print the values $n_i$ for the points in that subset, one per line.

If there are multiple valid partitions, you may choose any of them. You may print either of its two subsets, and you may list the subset's $n_i$ values in any order.

4
-0.950000 -0.850000
-0.100000 0.999999
0.111000 0.555000
-0.200000 1.600000

3
0
-1
-1

3
0.500000 0.700000
0.100000 0.200000
0.800000 0.900000

0

4
-360.000001 -24.000001
-359.999999 -24.000001
-359.999999 -23.999999
-360.000001 -23.999999

2
-25
-360

提示

Sample Input 1 is shown in the image below:

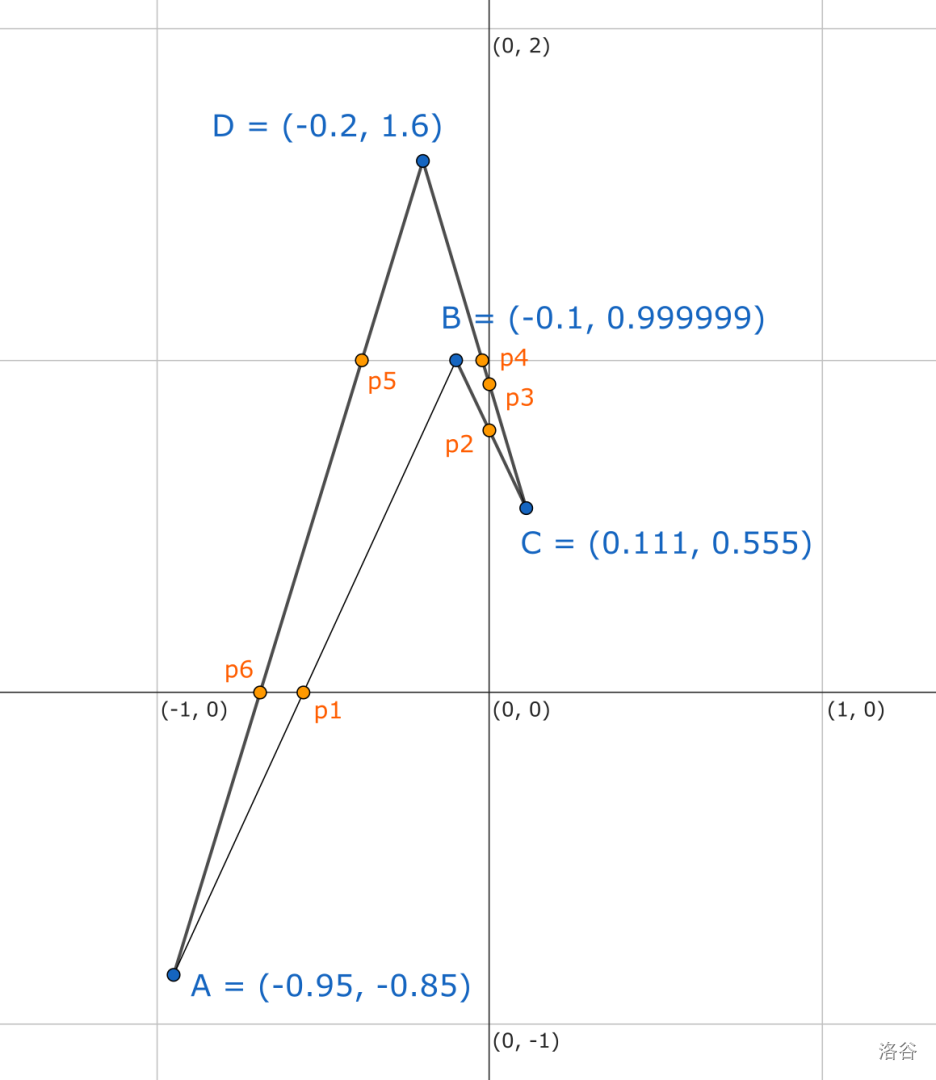
The points of the vertices are labeled $A,B,C,D$. The semi-integer points are marked in orange and labeled $p_i$ going counterclockwise around the perimeter starting from $A$. The values $n_i$ of the semi-integer points are, in the same order, $-1, 0, 0, -1, -1, -1$. Any subset of those values that sum to $-2$ would be accepted as correct. Sample Output 1 shows one possible correct answer.

The boundary of the polygon in Sample Input 2 does not intersect any semi-integer points, so $\mathcal{P}$ is empty, and it can be partitioned into two empty sets each with $n_i$ sum of zero.