题目描述

The government of the Independent Country of Problem Creators (ICPC) finally saved enough money to construct high speed rail infrastructure. The new rail system has $V$ stations and $E$ bidirectional direct railway lines that each connect two stations together. The head of ICPC Rail Infrastructure Planning, Skib E. Dee, has seen enough programming problems about tree-topology transportation networks in other countries to know that such a network would be a recipe for disaster: a single broken railway line would split the network into disconnected pieces and disrupt travel for days. Instead, Dee decided that the ICPC rail network will be robustly connected: every pair of stations $s_1$, $s_2$ must be connected by at least two paths which do not share any direct railway lines, and do not share any railway stations other than $s_1$ and $s_2$ themselves.

Of course, ICPC cannot afford to build too many redundant railway lines. To balance efficiency and resiliency, Dee has also designed the network to be regionally connected. A cycle is a non-empty path from a station to itself which doesn't repeat any railway station (apart from the first station, which must repeat exactly once as the last station of the cycle). In order for the network to be regionally connected, there must exist a set $\mathcal{F}$ of $E-V+1$ regional cycles satisfying three properties:

• every direct railway line in the transportation network belongs to at least one regional cycle;
• if two regional cycles share any direct railway lines, then all railway lines and stations shared by those cycles lie along a connected path;
• for each subset $f$ of $\mathcal{F}$, at most $|f|-1$ pairs of regional cycles in $f$ share any direct railway lines.

To promote the new high speed rail, Dee needs to create a timelapse video of a train travelling around some cycle in the railway network. Each direct railway line has a (possibly negative) scenic value representing how nice the view out the train window is along that line. Dee wants to send the train around whichever cycle maximizes the sum of scenic values of the direct railway lines on the cycle---compute this maximum possible sum. (The most scenic cycle that Dee is looking for does not have to be a regional cycle.) In order to ensure this cycle is not boring, it must traverse at least two direct railway lines, and must not repeat any railway station (apart from the first station, which must repeat exactly once as the last station of the cycle).

输入格式

The first line of input contains two space-separated integers $V$ ($2\leq V \leq 2 \cdot 10^5$) and $E$ ($V \leq E \leq 4 \cdot 10^5$), the number of stations and direct railway lines in the rail network, respectively.

The next $E$ lines of input describe the direct railway lines. Each line contains three space-separated integers $a$, $b$, and $s$ ($1\leq a,b \leq V$; $-10^9 \leq s \leq 10^9$), signifying that a direct railway line exists between stations $a$ and $b$ with scenic value $s$. No direct railway line connects a station to itself, but multiple direct railway lines might exist between the same two stations. It is guaranteed that the input graph will be both robustly connected and regionally connected.

输出格式

Print the sum of scenic values around the cycle in the railway network that maximizes this sum.

6 9
1 2 9
2 3 9
3 4 9
3 4 -9
4 1 9
1 5 1
5 6 1
6 2 1
3 4 8

36

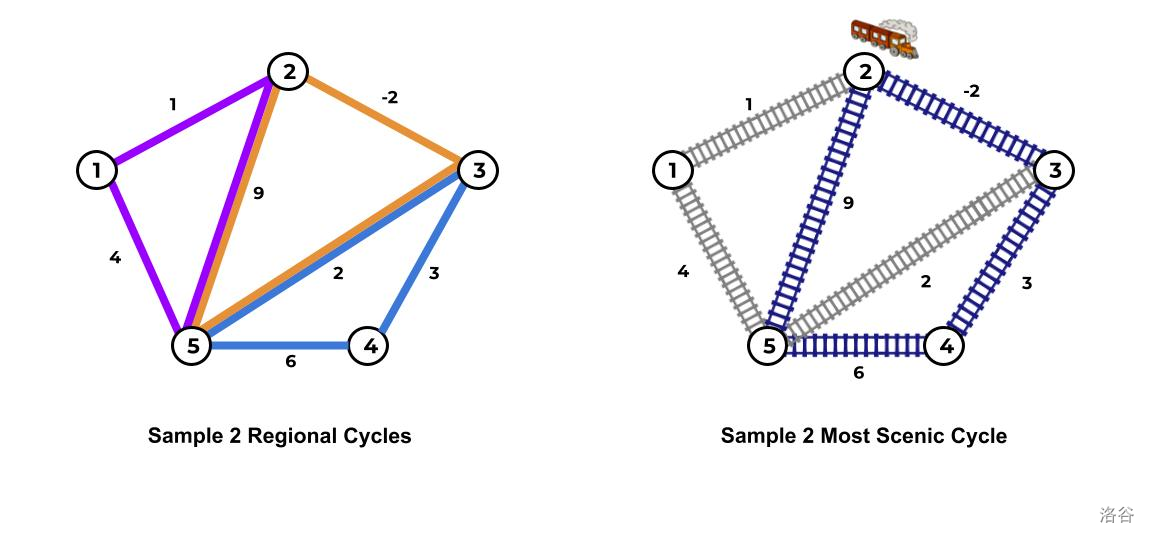
5 7
1 2 1
2 3 -2
3 4 3
4 5 6
5 1 4
5 3 2
2 5 9

16

提示

For the railway network in Sample Input 2, one possible choice for the regional cycles in $\mathcal{F}$ are $1 \rightarrow 2 \rightarrow 5 \rightarrow 1$, $2 \rightarrow 5 \rightarrow 3 \rightarrow 2$, and $3 \rightarrow 4 \rightarrow 5 \rightarrow 3$ (pictured on the left). The most scenic cycle (pictured on the right, in blue) has a scenic value sum of $9+6+3-2 = 16$.