题目背景

Ouroboros from Wikimedia Commons

题目描述

Your friend has given you a rooted tree: a connected graph with $N$ nodes and $N-1$ edges. The nodes of the tree are numbered from $1$ to $N$, with node $1$ being the root of the tree and other nodes numbered arbitrarily.

However, you recently learned about the Ouroboros, an ancient mythical snake that eats its own tail, signifying a cycle with no beginning and end. You dislike the fact that the tree you were given has a very clear beginning at the root, and clear ends at its leaves, so you decide to completely change the structure of this tree into a new graph which you have named an Ouroboros Graph.

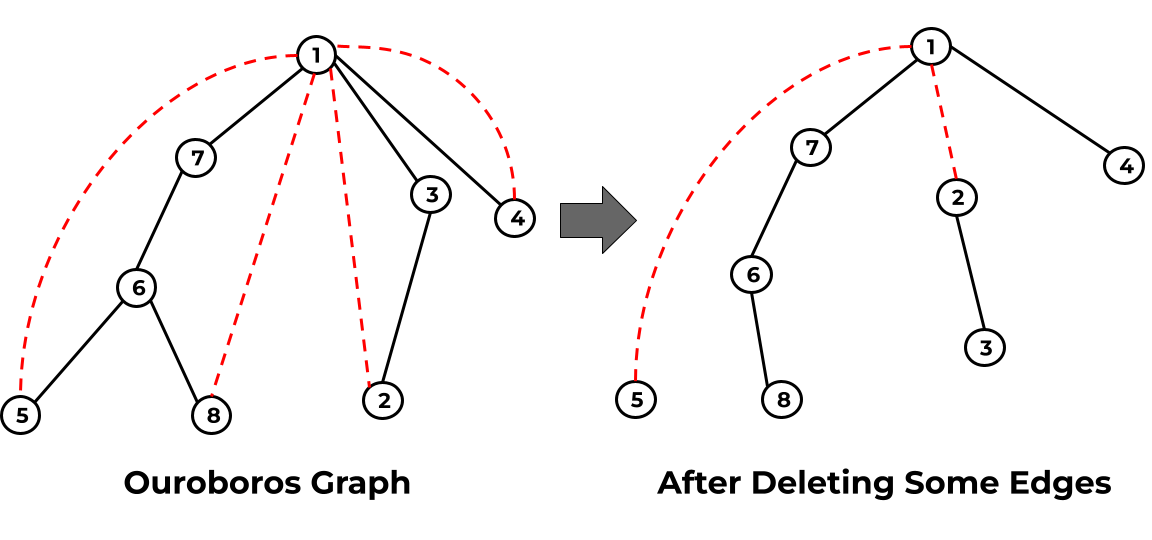
To construct this Ouroboros Graph, you take the leaves of the tree (the nodes with no direct children) and draw special "leaf" edges that connect every leaf directly to the root. If there is already an edge connecting a leaf to the root, you still add a duplicate edge.

With this special graph structure, you can now create lots of different trees by removing some subset of edges, and in the spirit of Ouroboros, the leaves and roots can change depending on which subset of edges you remove. How many different trees can you make by removing a subset of edges from the Ouroboros Graph? Two trees are considered different if one tree has an edge that the other tree does not. (If both a regular and a "leaf" edge connect the same pair of nodes, then they are distinguishable from each other and are considered different edges.) Since the number of trees can be large, compute the answer modulo $998\,244\,353$.

输入格式

The first line of input contains a single integer $N$ ($2 \leq N \leq 200\,000$), the number of nodes in the tree.

Each of the next $N-1$ lines contains two space separated integers $a$ and $b$ ($1 \leq a,b \leq N$) specifying that an edge exists between parent node $a$ and child node $b$ in the tree. The input graph is indeed guaranteed to be a tree: there is a unique path of edges between every pair of nodes in the graph.

输出格式

Print the number of different trees modulo $998\,244\,353$ that can be created by removing some subset of edges from the input tree's Ouroboros Graph.

8
1 3
3 2
1 4
1 7
7 6
6 5
6 8

72

提示

In the diagram below, the left subfigure illustrates the Ouroboros Graph corresponding to Sample Input 1, with the original edges of the tree drawn in black and the "leaf" edges dashed in red. The tree on the right illustrates one of the $72$ possible different trees that can be formed by deleting some subset of edges from the Ouroboros Graph: in this case, original edges $6$--$5$ and $1$--$3$ and "leaf" edges $1$--$8$ and $1$--$4$ were deleted.