题目背景

请使用 C++17 或 C++20 提交本题

你需要在程序开头加入如下代码：

#include <string>

int polygon(std::string S);

题目译自 2019년도 국제정보올림피아드 대표학생 선발고사 - 2차 선발고사 T4「다각형」

题目描述

考虑一个由水平和垂直边组成，并有 $N$ 个顶点的多边形 $P$。多边形 $P$ 的边只能在端点相交，每个顶点正好有两条边的端点相交。当沿着多边形 $P$ 的边逆时针移动时，会在顶点处向左或向右转弯。如果在顶点处向左转弯，用 $\texttt{L}$ 表示；向右转弯，则用 $\texttt{R}$ 表示。这样就可以用 $\texttt{L}$ 和 $\texttt{R}$ 组成的字符串来表示多边形。例如，图 1 中的多边形可以用字符串

$$\texttt{LLRLLRRLLRLLRLLRRLLR}$$

表示。用字符串表示多边形时，字符串的起始位置总是多边形最左边边的上方顶点。这个字符总是 $\texttt{L}$。

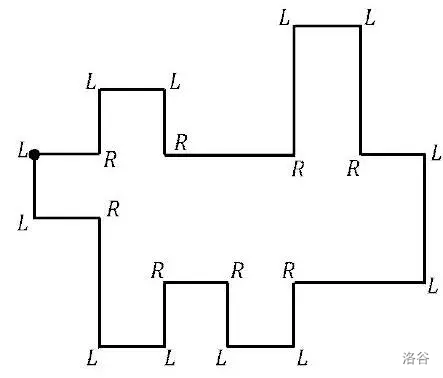
用给定字符串表示的多边形需要满足以下条件：对于任意垂直线 $V$，$V$ 在多边形水平边的内部（不包括端点）最多只能有 $2$ 个交点。

对于多边形 $P$，其包含的最小水平和垂直边组成的矩形记为 $B(P)$。它由多边形 $P$ 的最左、最右、最上和最下边与矩形的垂直和水平线重合（见图 2）。

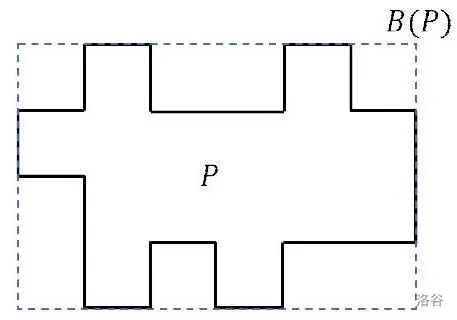
给定由字母 $\texttt{L}$ 和 $\texttt{R}$ 组成的长度为 $N$ 的字符串，绘制这个字符串表示的满足上述条件的多边形 $P$。此时，多边形 $P$ 的边长为整数。编写一个程序，使 $B(P)$ 的面积最小，并输出其最小值。

你需要为管理员实现以下一个函数：

• int polygon(string S);

接受长度为 $N$ 的字符串 $S$ 作为参数。字符串 $S$ 的每个字符是 $\texttt{L}$ 或 $\texttt{R}$。函数需要找到字符串 $S$ 表示的多边形 $P$ 中使 $B(P)$ 的面积最小的情况，并返回这个最小面积。

函数必须按照上述描述进行操作。当然，你可以创建和使用其他函数，但不得进行任何输入输出操作或访问其他文件。

输入格式

示例评测程序按以下格式读取输入：

• 第 $1$ 行：$N$，表示字符串的长度
• 第 $2$ 行：长度为 $N$ 的字符串 $c_{1} c_{2} \cdots c_{N}$，其中 $c_{1}=\texttt{L}, c_{i}=\texttt{L}$ 或 $\texttt{R} (2 \leq i \leq N)$

输出格式

示例评测程序会输出 polygon 函数的返回值。

8
LLLRRLLL

6

20
LLRLLRRLLRLLRLLRRLLR

15

提示

对于所有输入数据，满足：

• 输入字符串仅包含字母 $\texttt{L}$ 或 $\texttt{R}$
• 表示上述条件的多边形的输入字符串总是存在至少一个
• $4 \leq N \leq 800$

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制
$1$	$20$	$N \leq 10$
$2$	$36$	$N \leq 40$
$3$	$21$	$N \leq 100$
$4$	$73$	无附加限制