题目背景

请使用 C++17 或 C++20 提交本题

你需要在程序开头加入如下代码：

#include <vector>
long long findSum(int N, std::vector<int>C, std::vector<int> Node1, std::vector<int> Node2);

题目译自 2019년도 국제정보올림피아드 대표학생 선발고사 - 1차 선발고사 T1「트리」

题目描述

有一棵包含 $N$ 个节点的树 $T=(V, E)$。每个节点上写有一个整数（可以为负）。我们需要找到满足以下条件的两棵子图 $T_{a}=\left(V_{a}, E_{a}\right)$ 和 $T_{b}=\left(V_{b}, E_{b}\right)$：

• $V_{a} \neq \varnothing, V_{b} \neq \varnothing$；
• $T_{a}$ 和 $T_{b}$ 都是连通图；
• $V_{a} \cap V_{b}=\varnothing$；
• $E$ 中没有连接 $V_{a}$ 中节点和 $V_{b}$ 中节点的边；
• 最后，我们希望 $V_{a}$ 中所有节点的整数之和与 $V_{b}$ 中所有节点的整数之和的总和尽可能大。

考虑下面的例子：$T=(\{0,1,2,3,4,5,6\},\{(0,1),(0,2),(2,3),(2,4),(4,6),(5,6)\})$。

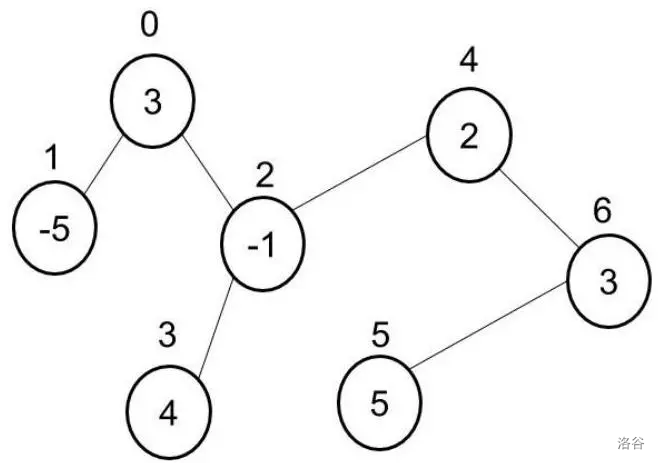
节点上的数字表示节点编号，节点内的数字表示该节点上的值。可以有多种方法找到符合条件的 $T_{a}$ 和 $T_{b}$，但选择 $V_{a}=\{0,2,3\}$ 和 $V_{b}=\{5,6\}$，两个子图中的整数和为 $\{3+(-1)+4\}+\{5+3\}=14$，这是最大的值。虽然有其他方法，但无法得到比 $14$ 更大的值。

你需要实现以下函数：

long long findSum(int N, int C[], int Node1[], int Node2[]);

该函数将会被调用一次，传入输入参数并返回问题的答案。$N$ 表示节点数，节点编号从 $0$ 到 $N-1$。编号为 $i (0\leq i\leq N-1)$ 的节点上写的数为 $C_i$。编号为 $Node1_i$ 和 $Node2_i (0\leq i\leq N-2)$ 的节点由一条边连接。

这些函数必须按照上述描述工作。当然，你可以创建其他函数并在内部使用。提交的代码不得进行输入输出操作或访问其他文件。

输入格式

示例评测程序将按照以下格式读取输入：

• 第 $1$ 行：$N$
• 第 $2$ 行：$N$ 个整数 $C_{0}, C_{1}, \ldots, C_{N-1}$，表示每个节点的值。
• 接下来的 $N-1$ 行：两个整数 $a$ 和 $b$，表示编号为 $a$ 和 $b$ 的节点由边连接。

注意：每行最后一个数字后面不得有空格或其他字符，否则示例评测程序可能无法正确工作。

输出格式

示例评测程序将输出 findSum() 函数的返回值。

7
3 -5 -1 4 2 5 3
0 1
0 2
2 3
2 4
4 6
5 6

14

提示

对于所有输入数据，满足：

• $-10^{9} \leq C_{i} \leq 10^{9}$
• $3 \leq N \leq 5\cdot 10^5$

详细子任务附加限制及分值如下表所示。