题目描述

On her birthday, Lady received a gift --- a network. The network contains $n$ nodes, numbered with integers from $1$ to $n$. Each node is assigned a specific letter, denoted as $s_i$ for the node with number $i$.

There are one-way connections between some pairs of nodes. Each node has exactly one outgoing one-way connection. Let the connection for the node with number $i$ lead to the node with number $x_i$. Note that $x_i$ can be equal to $i$ --- in this case, it is considered that the connection from the node with number $i$ leads to the same node.

Let $p_{i,0} = i$ and $p_{i,k} = p_{x_i,k-1}$. Thus, $p_{i,k}$ is the number of the node where a chip will end up if it is placed in the node with number $i$ and moved along the connection from the current node $k$ times.

Lady created a matrix $a$ of size $n\times (3\cdot n)$, where $a_{i,j} = s_{p_{i,j-1}}$. Thus, the $i$-th row of the matrix $a$ is a sequence of $3\cdot n$ letters, where the first letter equals $s_i$, the second letter equals $s_{x_i}$, the third equals $s_{x_{x_i}}$, and so on.

Lady informed some rows of the matrix $a$ and asks you to construct any network that corresponds to the known rows of the matrix $a$.

输入格式

The first line contains a single integer $n$ $(1 \leq n \leq 2\cdot{10}^3)$ --- the number of nodes in the network.

The next $n$ lines describe the matrix $a$. Each of these lines contains $3\cdot n$ lowercase Latin letters, representing the corresponding row of matrix $a$, or a single symbol $\tt{?}$ if Lady did not inform the corresponding row.

It is guaranteed that there exists at least one network that satisfies the given conditions.

输出格式

In the first line, output a string $s$ consisting of $n$ lowercase Latin letters --- the letters written on the nodes of the network.

In the second line, output $n$ integers $x_1, x_2, \ldots, x_n$ $(1 \leq x_i \leq n)$ --- the numbers of the nodes to which the connections from the corresponding nodes lead.

The matrix corresponding to this network must be exactly equal to the matrix $a$ in all rows that Lady informed.

If there are multiple correct answers, you are allowed to output any of them.

4
abaaaaaaaaaa
baaaaaaaaaaa
aaaaaaaaaaaa
cccccccccccc

abac
2 3 3 4

3
axaxaxaxa
xxxxxxxxx
?

axx
3 2 1

提示

In the first example, $x_1 = 2$ and $x_2 = 3$, so $p_{1,0}=1, p_{1,1}=2, p_{1,2}=3$. Since $x_3=3$, all $p_{1,k}$ for $k\geq3$ are also equal to $3$. Accordingly, the second letter of the first row equals $s_2$, and the third equals $s_3$.

Below are the images of networks from the examples. The numbers in the corners indicate the node numbers, the letters indicate the values written on the corresponding nodes, and the arrows indicate the one-way connections.

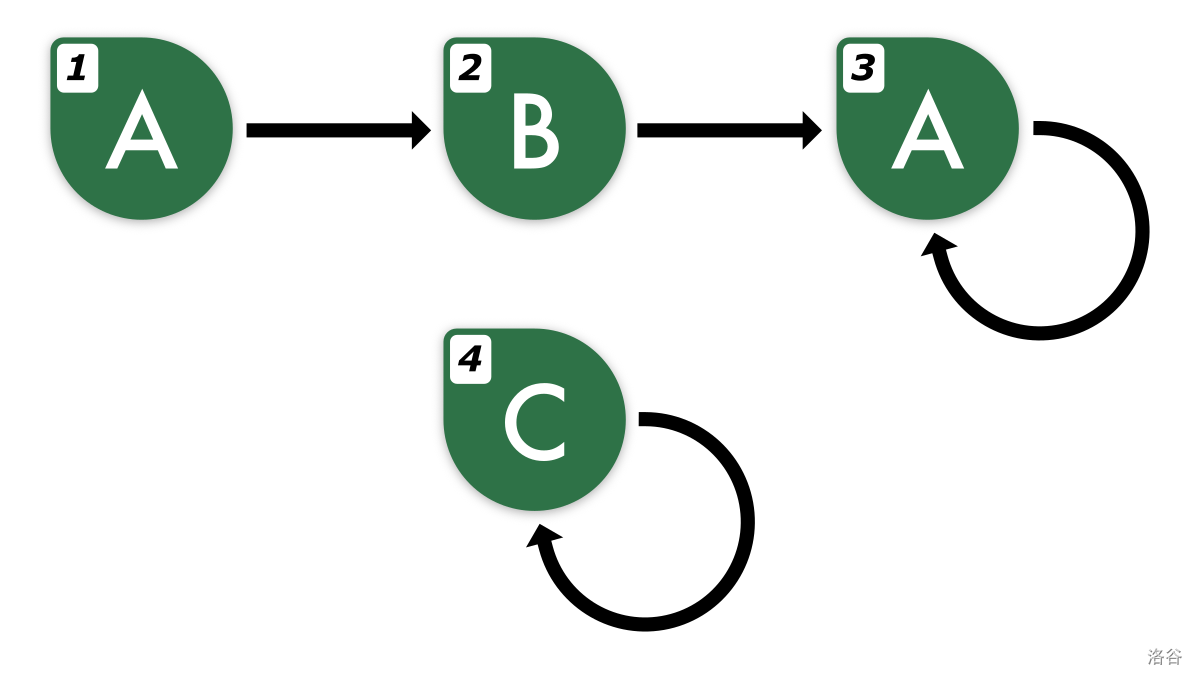
Network from the first example

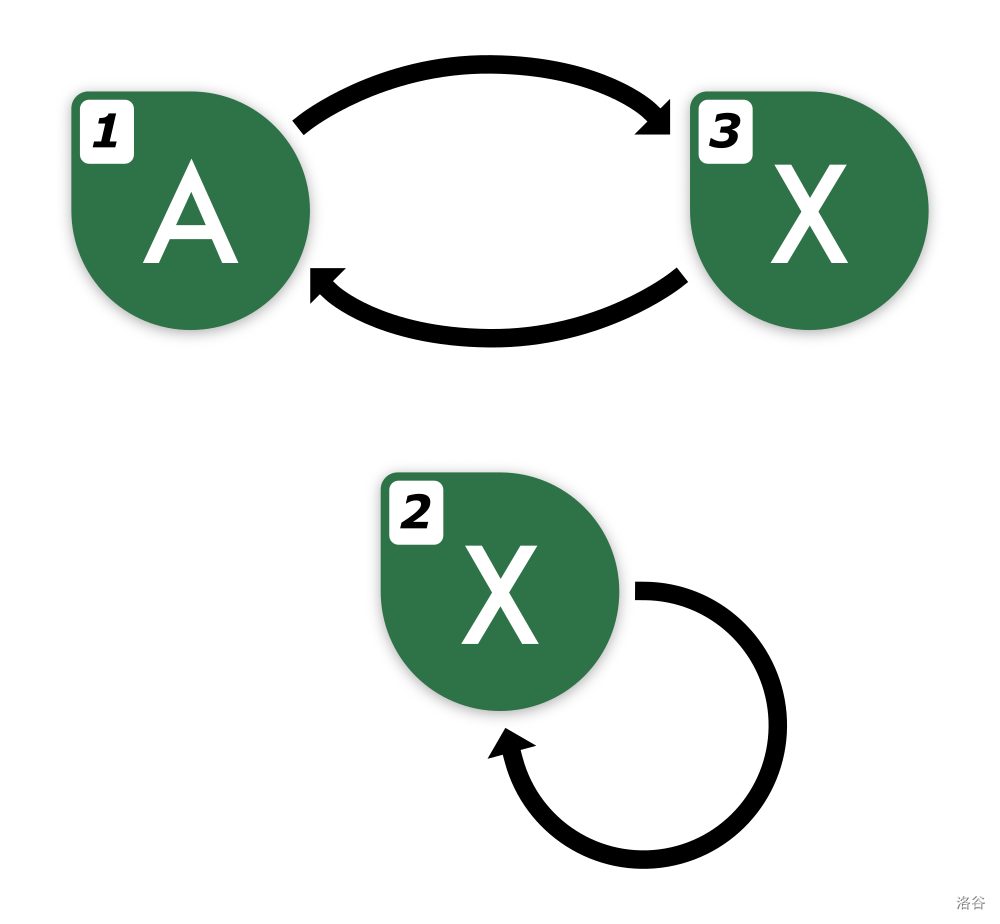
Network from the second example

Scoring

Let $q$ be the number of rows that Lady did not inform.

We call a network a set of pairs and unit nodes if the network can be divided into nodes, from which the connection leads to itself (i.e., $x_v = v$), and pairs of nodes $(a,b)$ such that $x_a=b$ and $x_b=a$.

We call a network a set of stars if the network can be divided into separate stars, each of which consists of a main node $v$, from which the connection leads to itself (i.e., $x_v = v$), and a set of secondary nodes $y=\{y_1, y_2, \ldots, y_k\}$ such that $x_{y_i}=v$ for $1 \leq i \leq k$. Note that the stars in the network may have different sizes and consist only of one main node.

We call a network a tree with the root at node $v$ if from node $v$ the connection leads to itself (i.e., $x_v = v$), and for each other node it is possible to reach node $v$ using the network connections (i.e., for each $1 \leq i \leq n$ there is such $k$ that $p_{i,k}=v$).

We call a network a cycle if starting from any node it is possible to reach any other node using the network connections (i.e., for all $1 \leq i,j \leq n$ there is such $k$ that $p_{i,k}=j$).

• ($10$ points): $n \leq 5$, $q = 0$;
• ($6$ points): $n \leq 300$, $q = 0$, $x_{x_i}=i$ for $1\le i\le n$ (the network is a set of pairs and unit nodes);
• ($6$ points): $n \leq 300$, $q = 0$, $x_{x_i}=x_i$ for $1\le i\le n$ (the network is a set of stars);
• ($9$ points): $n \leq 300$, $q = 0$, $x_1=1$ and $x_i<i$ for $2\le i \le n$ (the network is a tree with the root at node $1$);
• ($9$ points): $n \leq 300$, $q = 0$, for all $1 \leq i,j \leq n$ there is such $k$ that $p_{i,k}=j$ (the network is a cycle);
• ($13$ points): $n \leq 300$, $q = 0$;
• ($25$ points): $n \leq 300$;
• ($10$ points): $n \leq 2\cdot{10}^3$, $q = 0$;
• ($12$ points): without additional restrictions.