题目描述

Asadullo is an outstanding researcher at APIO (Alliance for Power and Industrial Optimization). Recently, he has been studying a method to generate energy using an unknown material.

This unknown material does not produce energy on its own, but if there are several extremely long rods made of this material, they can generate energy through their interactions.

Specifically, there are $n$ rods, given by an array $v[0], v[1], \ldots, v[n-1]$. The $i$-th rod can be positioned at an angle of $a[i] = 360 \cdot \frac{v[i]}{100000}$, with respect to the positive direction of the x-axis, in counterclockwise. The energy efficiency by these $n$ rods is defined as

$$\sum_{i<j} \text{acute}(i,j)$$

where $\text{acute}(i,j)$ represents the acute angle formed between the $i$-th rod and the $j$-th rod. In this problem, we consider $90^\circ$ as an acute angle.

More formally, $\text{acute}(i,j) = \min(|v[i] - v[j]|, 50000 - |v[i] - v[j]|)$.

In other words, the energy efficiency is calculated by adding the acute angles between every pair of rods.

For example, if $v = [5000, 12500, 37500]$ and correspondingly, $a = [18, 45, 135]$, we would get the following graph:

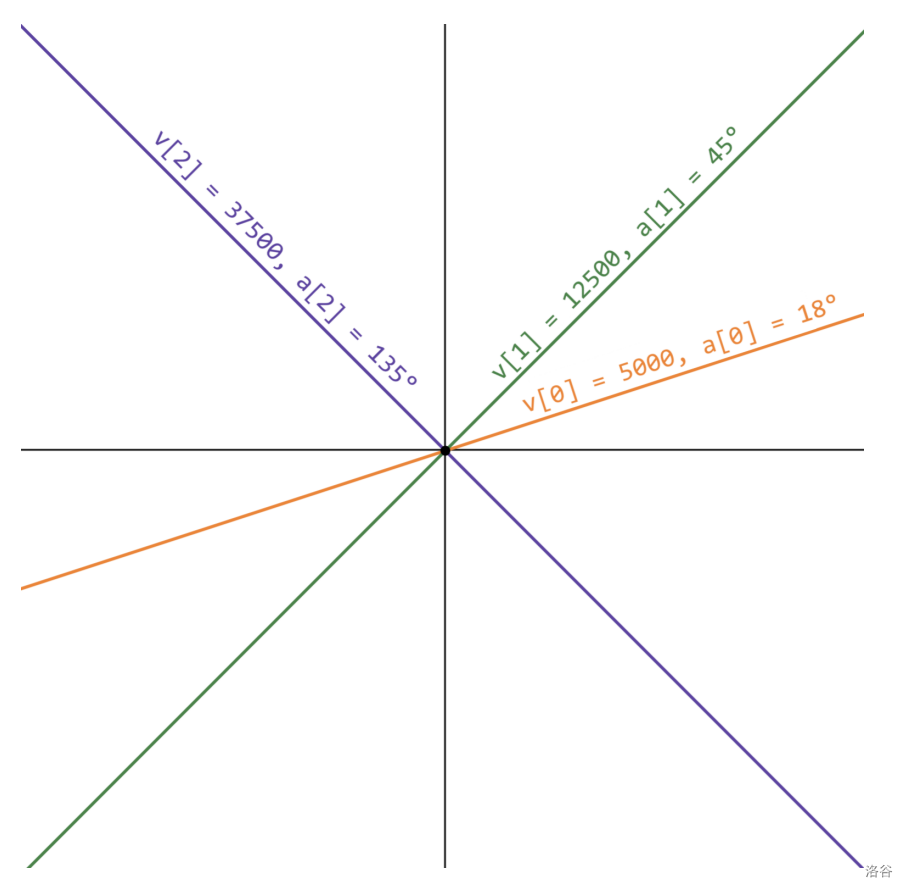
Here, acute(0, 1) = 7500 (i.e. 27°), acute(0, 2) = 17500 (i.e. 63°), and acute(1, 2) = 25000 (i.e. 90°). Therefore, the energy efficiency of these rods equals $7500 + 17500 + 25000 = 50000$.

Asadullo wants to adjust the arrangement of these $n$ rods to maximize their energy efficiency. However, there are several constraints:

• First, since this material is extremely hazardous to living beings, the rods can only be rotated using a specialized mechanical device in a controlled manner. This device allows selecting multiple rods at once and rotating them by the same angle simultaneously.
• Asadullo does not want the energy efficiency of the rods to decrease. Therefore, after any operation using the device, the energy efficiency must not be lower than before.
• Since operating the device consumes a large amount of energy, the total number of rods selected across all operations must not exceed 2 000 000.

Under these constraints, Asadullo wants to perform operations optimally to maximize the energy efficiency of the rods. Write a program to help Asadullo achieve the highest possible energy efficiency.

Implementation details

You should implement the following procedure:

void energy(int n, std::vector<int> v)

• $n$: the number of rods.
• $v$: an array of length $n$ containing information about the rods.
• This procedure is called exactly once.

Within this procedure, you may call the following procedure:

void rotate(std::vector<int> t, int x)

• $t$: an array of distinct indices, i.e. $0 \leq t[i] < n$ for each $i$ and $t[i] \neq t[j]$ for each $i < j$. Array $t$ is not required to be sorted.
• This procedure rotates every rod which index is given in the array $t$ by parameter $x$, simultaneously. That is, $v[i]$ becomes $(v[i] + x) \mod 50000$ for every index $i$ which is present in $t$.
• This procedure can be called multiple times. The total length of $t$ over all calls must not exceed 2 000 000.

提示

Examples

Example 1

Consider the following call:

energy(2, [20000, 10000])

Here, $v = [20000, 10000]$ and the initial energy efficiency equals $20000 - 10000 = 10000$. One of the possible scenarios is the following:

• call rotate([0, 1], 8000). Then $v$ becomes $[28000, 18000]$. The energy efficiency stays the same.
• call rotate([0], 15000). Then $v$ becomes $[43000, 18000]$. The energy efficiency becomes $43000 - 18000 = 25000$.

It can be shown that for the given input, 25000 is the maximum possible energy efficiency. Therefore, Asadullo can stop performing these operations.

Example 2

Consider the following call:

energy(3, [5000, 12500, 37500])

The image for this example was presented above. It can be shown that the initial energy efficiency is the maximum possible. Thus, no operations are needed.

Constraints

• $2 \leq n \leq 100 \, 000$
• $0 \leq v[i] \leq 49 \, 999$ for each $0 \leq i < n$
• elements of $v$ are not necessarily distinct

Subtasks

1. (5 points) $n = 2$
2. (11 points) $v[i] < 25 \, 000$ for each $0 \leq i < n$
3. (8 points) $n \leq 10$
4. (15 points) $n \leq 100$
5. (15 points) $n \leq 300$
6. (20 points) $n \leq 2000$
7. (26 points) No additional constraints.

Sample Grader

The sample grader reads the input in the following format:

• line 1: $n$
• line 2: $v[0] \, v[1] \ldots \, v[n - 1]$

The sample grader prints the output in the following format:

• line 1: final energy efficiency of rods

Also, the grader will write detailed information about the rotations you made in the file log.txt.