题目描述

Alice and Bob are childhood friends, and they love playing intellectual games. Today, they are playing a new game on graphs.

The game set contains a connected graph with $m$ vertices, numbered from $0$ to $m-1$, and $e$ edges, numbered from $0$ to $e-1$. The $i$-th edge connects vertices $u[i]$ and $v[i]$.

The game set also contains a permutation $p[0], p[1], \ldots, p[n-1]$ of length $n$, where $m \leq n$. Permutation is an array in which each number from $0$ to $n-1$ appears exactly once, in some order. The score of permutation $p$ is the number of indices $i$ such that $p[i] = i$.

The game will last for at most $10^{100}$ turns. In each turn, the following happens:

1. If Alice decides to end the game, the game stops.
2. Otherwise, Alice chooses distinct indices $t[0], t[1], \ldots, t[m-1]$, where $0 \leq t[i] < n$. Note that, the game does not require $t[0] < t[1] < \ldots < t[m-1]$.
3. Bob chooses an index $0 \leq j < e$ of the edges of the graph and swaps $p[t[u[j]]]$ and $p[t[v[j]]]$.

Alice wishes to maximize the final score of the permutation while Bob wishes to minimize the final score of the permutation.

Your task is to help Alice and play against Bob, whose moves are simulated by grader.

Let's define optimal score as the final score of the permutation if both Alice and Bob play optimally.

You will need to determine the optimal score of the permutation and then play the game with Bob to achieve at least that optimal score after some turns.

Note that Alice's strategy should work no matter what moves Bob makes, including if Bob makes unoptimal moves.

Implementation details

You should implement the following procedure:

int Alice(int m, int e, std::vector<int> u, std::vector<int> v,
    int n, std::vector<int> p)

• m: the number of vertices in the graph.
• e: the number of edges in the graph.
• u and v: arrays of length e describing the edges of the graph.
• n: the length of the permutation.
• p: an array of length n describing the permutation.

This procedure is called exactly once. This procedure should return an integer – the optimal score of the game. Within this procedure, you may call the following procedure:

int Bob(std::vector<int> t)

• t: an array of size m, containing distinct indices, where $0 \leq t[i] < n$ and $t[i] \neq t[j]$ for any $i \neq j$. This function returns a single integer j which satisfies $0 \leq j < e$. This procedure can be called multiple times.

提示

Example

Consider the following call:

Alice(5, 6, [4, 0, 3, 1, 4, 2], [2, 2, 0, 2, 0, 3], 
10, [8, 2, 7, 6, 1, 5, 0, 9, 3, 4])

The graph is as follows:

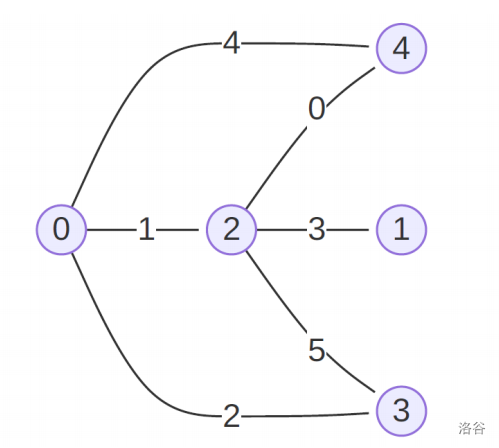
and p is initially [8, 2, 7, 6, 1, 5, 0, 9, 3, 4]. Given the constraints above, we can prove that the optimal score of the permutation is 1.

Suppose, Alice makes the following 4 moves:

Argument of t to Bob	Return value of Bob	Corresponding indices of p	p after the swap by Bob
[3, 1, 5, 2, 0]	5	5, 2	[8, 2, 5, 6, 1, 7, 0, 9, 3, 4]
[9, 3, 7, 2, 1]	0	1, 7	[8, 9, 5, 6, 1, 7, 0, 2, 3, 4]
[5, 6, 7, 8, 9]	1	5, 7	[8, 9, 5, 6, 1, 2, 0, 7, 3, 4]
[7, 5, 2, 3, 6]	3	5, 2	[8, 9, 2, 6, 1, 5, 0, 7, 3, 4]

Note that Alice and Bob not necessarily making the optimal moves. These moves are shown purely for demonstration purposes. Also note that Alice could finish the game immediately, as the initial score of the permutation is already 1.

After Alice has performed all the moves above, the actual score of the permutation is 3 ($p[2] = 2$, $p[5] = 5$, $p[7] = 7$). Finally, the function Alice() will return 1 – the optimal score of the permutation.

Note that even though Alice has achieved a score of 3 by playing with Bob, you would get 0 points if the return value of Alice() was 3 instead of 1.

Constraints

• $2 \leq m \leq 400$
• $m - 1 \leq e \leq 400$
• $0 \leq u[i], v[i] < m$
• $m \leq n \leq 400$
• $0 \leq p[i] < n$
• The graph is connected, contains no self-loops or multiple edges.
• $p$ is a permutation, i.e. $p[i] \neq p[j]$ for any $i \neq j$.

Subtasks

1. (6 points) $m = 2$
2. (6 points) $e > m$
3. (10 points) $e = m - 1$
4. (24 points) $e = m = 3$
5. (24 points) $e = m = 4$
6. (30 points) $e = m$

For each subtask, you can get partial score. Let $r$ be the maximum ratio of $\frac{k}{n}$ among all test cases of a subtask, where $k$ is the number of turns (i.e. calls to Bob()). Then, your score for that subtask is multiplied by the following number:

Condition	Multiplier
$12 \leq r$	$0$
$3 < r < 12$	$1 - \log_{10}(r - 2)$
$r \leq 3$	$1$

In particular, if you solve the problem within $3n$ turns, you get full points for that subtask. Using more than $12n$ turns results in getting 0 for that subtask (shown as Output isn't correct).

Sample Grader

The sample grader reads the input in the following format:

• line 1: $m$ $e$
• line 2 + $i$ ($0 \leq i \leq e - 1$): $u[i]$ $v[i]$
• line 2 + $e$: $n$
• line 3 + $e$: $p[0]$ $p[1]$ $\ldots$ $p[n - 1]$

The sample grader prints the output in the following format:

• line 1: final permutation $p$
• line 2: return value of Alice()
• line 3: actual score of final permutation
• line 4: the number of turns