题目描述

精灵古树是尼博尔山的生命之源，其根系中流淌的流光维系着整片森林的生态平衡。古树的躯体由 $n$ 枚光之核心构成，这些璀璨如星的光点通过 $n−1$ 条能量枝干交织成无环的树状脉络。任意两枚核心之间，都有一条唯一的能量枝干通道蜿蜒相连，仿佛命运编织的丝线。

而奥日，本是古树孕育的守护灵体，却在雷霆撕裂苍穹的雨夜，被狂暴的飓风卷入深渊。失去奥日的古树试图通过光之仪式呼唤他归来，但失控的能量反噬让它陷入永夜，原本澄澈的核心如今爬满黑暗的纹路。

如今，归来的奥日必须激活所有被侵蚀的核心：当他首次触碰某个核心时，纯净能量会驱散黑暗；但重复经过时，紊乱的能量将累计形成过载波动。古树的法则严苛限定------整条路径中，重复触发的波动总和不得超过 $k$ 次。

此刻，奥日悬浮在星网交织的虚空中。他可以从任意核心启程，沿着能量枝干的轨迹穿梭。奥日需要在蜿蜒的能量枝干间规划路径，在限制内点亮最多的核心。

唯有让尽可能多的光之核心重新共鸣，才能唤醒古树真正的力量，让治愈的流光再次奔涌在尼博尔山的每一片叶脉中！尼博尔山将迎来破晓，而黑暗，终会在这片星网的共振中灰飞烟灭……

形式化的，给定一个非负整数 $k$，给出一颗无根树 $T=(V,E)$，$V=\{1,2,\dots,n\}$。

定义一条由 $m$ 个可重点构成的路径 $l=(u_1,u_2,u_3,\dots,u_m)$ 满足：对于任意的 $1\le i\le m-1$ 有 $(u_i,u_{i+1})\in E$。如果存在 $1\le i<j\le m$，使得 $u_i=u_j$，则仍然认为 $l$ 是一条路径。

定义路径 $l$ 上的本质不同点集 $V'=\{v\mid v=u_i,\exists i\in [1, m]\}$。记 $|V'|$ 为集合 $V'$ 的大小。记路径 $l$ 上的重复点数量为 $s$，有 $s=m-|V'|$。

你需要找到一条路径 $l$，在满足 $s\le k$ 的情况下，最大化 $|V'|$。

你需要输出这条路径。如果存在多组路径满足条件，输出任意一条满足题意的路径，就会被认为正确。

输入格式

输入包含多个测试用例。数据的第一行包含一个整数 $t$ ($1 \leq t \leq 2\times 10^3$) 表示测试用例数。接下来描述每个测试用例。

每个测试用例的第一行包含两个整数 $n$ ($2\le n\le 2\times 10^5$) 和 $k$ ($0\le k\le n$)，用一个空格分隔，分别表示树上点的个数和可重复点数量的最大值。注意，$k$ 的取值可能为 $0$。

接下来 $n-1$ 行，每行两个正整数 $u$ 和 $v$ ($1\le u,v\le n$)，用一个空格分隔，表示树上存在一条边 $(u,v)$。保证该 $n-1$ 条边构成树。

保证所有测试用例的 $n$ 之和不超过 $2\times 10^5$。

输出格式

对于每个测试用例，输出两行。

第一行一个正整数 $m$，表示路径 $l$ 的可重点数量。路径 $l$ 需要在满足重复点数量 $s\le k$ 的情况下，最大化本质不同点集大小 $|V'|$。

第二行共 $m$ 个正整数 $u_1, u_2, u_3, \dots, u_m$，每个正整数之间用一个空格分隔，表示路径 $l$ 为 $(u_1, u_2, u_3, \dots, u_m)$。

如果存在多组路径满足条件，输出任意一条满足题意的路径，就会被认为正确。

可以被证明的，对于一个合法的路径，$m$ 一定有 $m\le n+k$。输出的 $m$ 一定要满足 $m \le n+k$，否则将直接返回 $\tt{Wrong\ Answer}$。

2
9 3
1 3
2 1
7 5
9 3
2 8
1 5
4 1
6 5
4 4
1 2
2 3
4 2

11
9 3 1 5 7 5 6 5 1 2 8
5
3 2 1 2 4

提示

对于第一组测试用例，$n=9$ 且 $k=3$，组成的树如下：

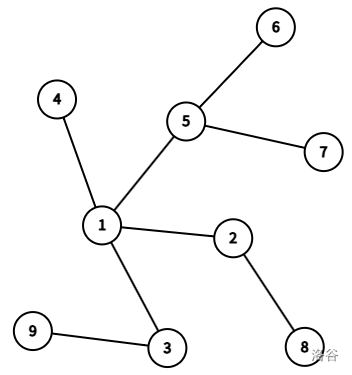
一组可行的解为：$l=(9,3,1,5,7,5,6,5,1,2,8)$。可以被证明的，此时本质不同点集大小 $|V'|$ 达到最大值 $8$，且重复点数量 $s=3\le k$。

对于第二组测试用例，$n=4$ 且 $k=4$，组成的树如下：

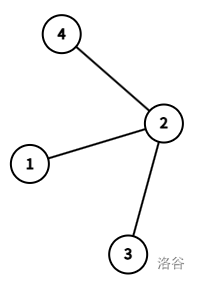
一组可行的解为：$l=(3,2,1,2,4)$。可以被证明的，此时本质不同点集大小 $|V'|$ 达到最大值 $4$，且重复点数量 $s=1\le k$。