题目背景

题目描述

定义从整点 $A$ 能看到整点 $B$，当且仅当 $A=B$，或者线段 $AB$ 上没有除 $A,B$ 外的任何整点。

现在给你 $n$ 个互不相同的点 $(x_i,y_i)$，设 $f(x,y)$ 表示在点 $(x,y)$ 处能看到的给定点的数量。给出 $X,Y$，求：

输入格式

第一行三个正整数 $X,Y,n$。

之后 $n$ 行，第 $i+1$ 行两个正整数 $x_i,y_i$。

输出格式

输出 $1\leq x\leq X,1\leq y\leq Y$ 时最多能看到的给定点的数量。

1 1 1
1 1

1

4 5 5
2 1
1 5
6 3
7 1
5 6

5

5 7 32
1 5
1 4
2 6
3 6
2 3
3 3
4 5
4 4
4 3
4 2
4 1
6 6
6 5
6 4
7 3
8 4
8 5
9 3
10 4
10 5
10 6
12 5
12 4
13 6
14 6
13 3
14 3
15 5
15 4
15 3
15 2
15 1

26

提示

样例解释 $2$：位于 $(2,2)$ 可以看到所有的点。

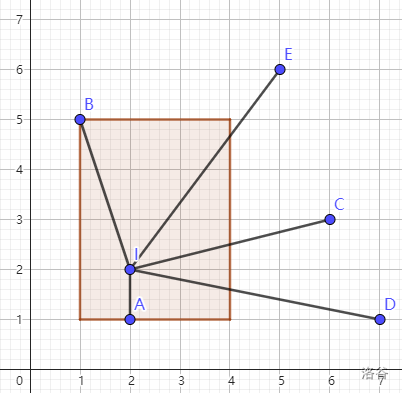
样例解释 $3$：位于 $(5,2)$ 可以看到 $26$ 个点。

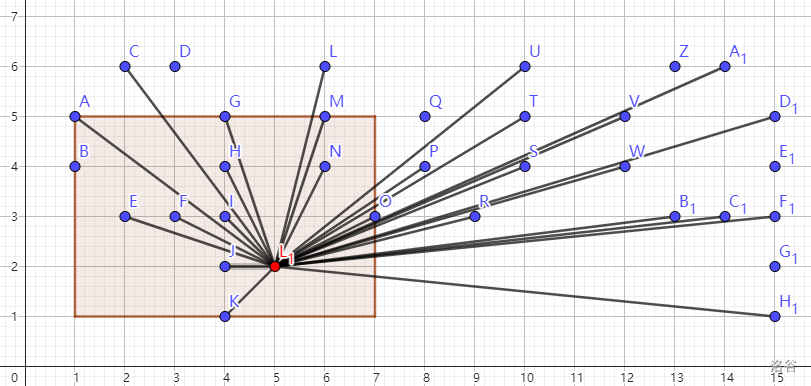
给定点中 $(1,4),(3,6),(8,5),(13,6),(15,2),(15,4)$ 无法从 $(5,2)$ 看见，因为其到 $(5,2)$ 的连线上有其它整点。

对于 $20\%$ 的数据，$1\leq X,Y,n\leq100$。

对于另外 $20\%$ 的数据，$1\leq X,Y\leq700,1\leq x_i,y_i\leq50$。

对于另外 $20\%$ 的数据，$1\leq X,Y\leq700$。

对于 $100\%$ 的数据，$1\leq X,Y,n,x_i,y_i\leq 2\times10^3$。