题目背景
由于评测机性能差异,本题时限增加了 3 秒。
题目描述
译自 ROI 2025 Day2 T3. Минимизация инверсий
你面前有一张 r 行 c 列的表格 a,里面填满了从 1 到 r⋅c 的所有不同数字,排列顺序完全随机。你的任务是将这些数字逐一转移到一个最初为空的数组 b 中。
只要表格还没清空,你可以重复以下两种操作之一:
- 操作 1:将表格第一行的元素按从左到右的顺序(从第一列到最后一列)添加到数组 b 的末尾,然后删除表格的第一行。
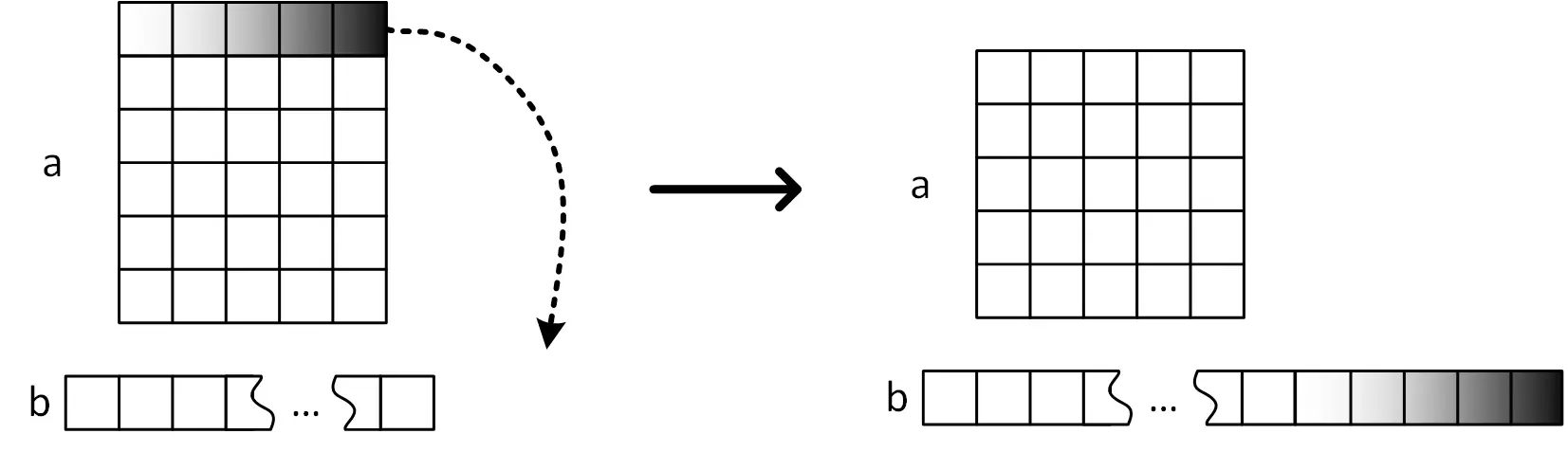
- 操作 2:将表格第一列的元素按从上到下的顺序(从第一行到最后一行)添加到数组 b 的末尾,然后删除表格的第一列。
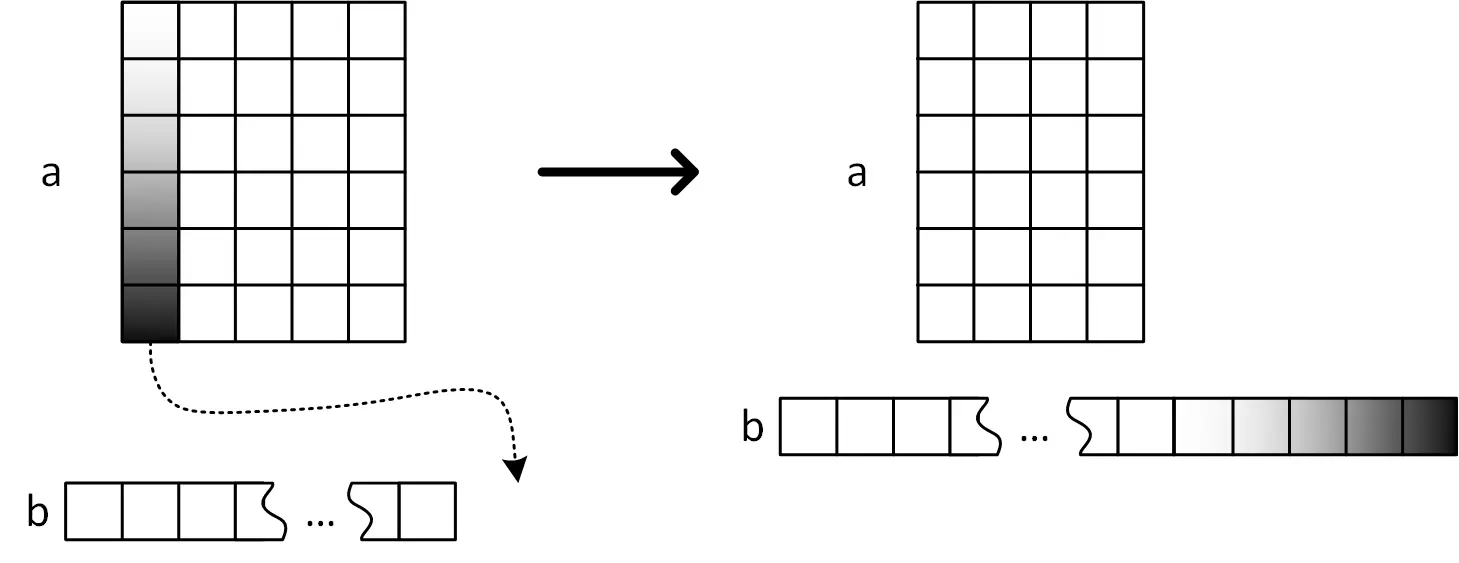
你需要巧妙选择操作的顺序,使得最终数组 b 中的逆序对数量最少。逆序对是指数组中满足 1≤i<j≤r⋅c 且 bi>bj 的索引对 (i,j)。
输入格式
第一行包含两个整数 r 和 c (r≤c,1≤r⋅c≤2000000),分别表示表格的行数和列数。
接下来的 r 行描述表格 a。第 i 行包含 c 个整数 ai1,…,aic (1≤aij≤r⋅c),表示表格第 i 行的元素。
保证表格 a 中的所有数字各不相同。
输出格式
输出一个整数,表示通过所有操作后,数组 b 中可能的最小逆序对数量。
2 3
3 4 1
5 6 2
6
2 3
2 3 4
1 6 5
2
提示
样例解释 1
在第一个样例中,最小逆序对数量可以通过两次删除第一行实现。最终数组 b 为 [3,4,1,5,6,2],包含 6 个逆序对。
样例解释 2
在第二个样例中,为了达到最小逆序对数量,可以先删除第一列,再两次删除第一行。最终数组 b 为 [2,1,3,4,6,5],包含 2 个逆序对。
详细子任务附加限制及分值如下表所示。其中子任务 0 是样例。
| 子任务 |
分值 |
附加限制 |
| 0 |
样例 |
| 1 |
15 |
r+c≤14 |
| 2 |
18 |
r⋅c≤500 |
| 3 |
5 |
所有行和列按升序排列,r⋅c≤250000 |
| 4 |
7 |
r=1,r⋅c≤250000 |
| 5 |
6 |
r≤2,r⋅c≤250000 |
| 6 |
2 |
r≤20,r⋅c≤250000 |
| 7 |
10 |
r,c≤100 |
| 8 |
2 |
r⋅c≤10000 |
| 9 |
1 |
r≤100,c≤1000 |
| 10 |
r≤100,c≤2500 |
| 11 |
r≤100,c≤5000 |
| 12 |
r≤100,c≤7500 |
| 13 |
r≤100,c≤10000 |
| 14 |
4 |
r≤100,c≤15000 |
| 15 |
2 |
r≤100,c≤20000 |
| 16 |
3 |
r,c≤200 |
| 17 |
r,c≤400 |
| 18 |
4 |
r,c≤600 |
| 19 |
1 |
r,c≤800 |
| 20 |
r,c≤1000 |
| 21 |
r,c≤1200 |
| 22 |
r,c≤1400 |
| 23 |
r⋅c≤100000 |
| 24 |
r⋅c≤250000 |
| 25 |
4 |
r⋅c≤500000 |
| 26 |
1 |
r⋅c≤750000 |
| 27 |
r⋅c≤1000000 |
| 28 |
r⋅c≤1500000 |
| 29 |
无附加限制 |


