题目描述

You are asked to help a team that participates in Innovation Workshop --- an event where teams of students invent and prototype their innovative ideas. One of the teams developed a new innovative washing machine that significantly reduces the usage of energy needed for laundry.

The innovative idea was to use a convex polygon instead of a circle for the shape of a washing machine drum. You are given this polygon. A drum is rotating around some fixed point inside the polygon with a constant speed of $1$ turn in $1$ second.

Currently, the prototype is built and testing is started. There are $s$ litres of water in the drum. At each moment of time, water under the influence of gravity occupies a region with area $s$ at the bottom of the drum.

Vertices of the polygon that are underwater are under pressure. By Pascal's law, we know that pressure is proportional to depth. Let's define by $d_1, d_2, \ldots, d_k$ depths of the vertices that are underwater at some moment of time, $k$ is the number of underwater vertices. Let's define the pressure imbalance as the average difference between underwater vertex depth and the maximum underwater vertex depth, i.e. $\frac{1}{k} \sum\limits_{i=1}^{k} \left(\max\limits_{j=1}^{k} d_j - d_i \right)$. Note that the order of $d_i$ is not important.

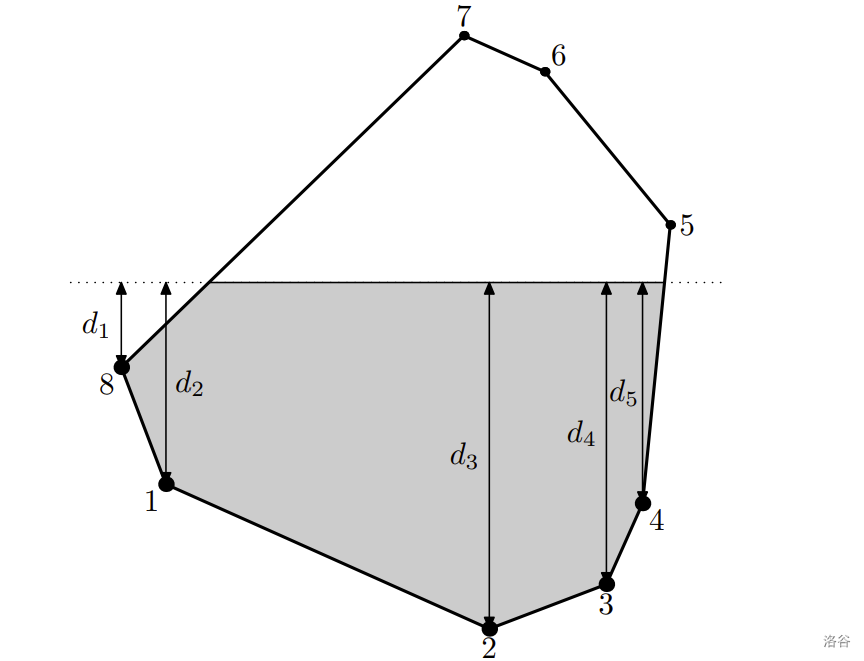
The polygon from the third test case is rotated. Vertices $1$, $2$, $3$, $4$, $8$ are underwater.

To select the optimal shape of the drum, the team wants to know the expected value of pressure imbalance for the moment of time selected uniformly from segment $[0, 1]$ (in seconds). Please help the team to calculate this value.

输入格式

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) --- the number of test cases. The next lines contain descriptions of test cases.

The first line contains two integers $n$, $s$ ($3 \leq n \leq 2 \cdot 10^5$, $s \geq 1$) --- the number of vertices in the polygon and the number of litres of water inside the drum. It is guaranteed that $s$ is less than the area of the polygon.

Each of the next $n$ lines contains two integers $x_i$, $y_i$ ($|x_i|, |y_i| \leq 10^8$) --- coordinates of polygon vertices.

It is guaranteed that the given points form a convex polygon. The area of the polygon is positive and no two consecutive segments are collinear. The vertices of the polygon are given in counterclockwise order.

The sum of $n$ for all test cases does not exceed $2 \cdot 10^5$.

输出格式

For each test case, print a single real number --- the expected value of pressure imbalance for a random uniform moment of time.

Your answer will be accepted if its absolute or relative error does not exceed $10^{-5}$; formally, if $p$ is your answer, and $j$ is the jury's answer, this should hold: $\frac{|p - j|}{\max\{1, |j|\}} \le 10^{-5}$.

4
4 2
0 0
2 0
2 2
0 2
3 1
1 -1
0 1
-1 -1
8 18
-2 1
-2 -3
-1 -4
0 -4
3 -3
4 -1
4 0
-1 2
4 1
99999998 99999999
99999999 99999998
100000000 99999999
99999999 100000000

0.3729232286
0.1379212354
1.3663189952
0.2636965438