题目描述

Saint Petersburg is the most beautiful city in the world unless it is raining. For the sake of this problem, we will assume it is raining every single day.

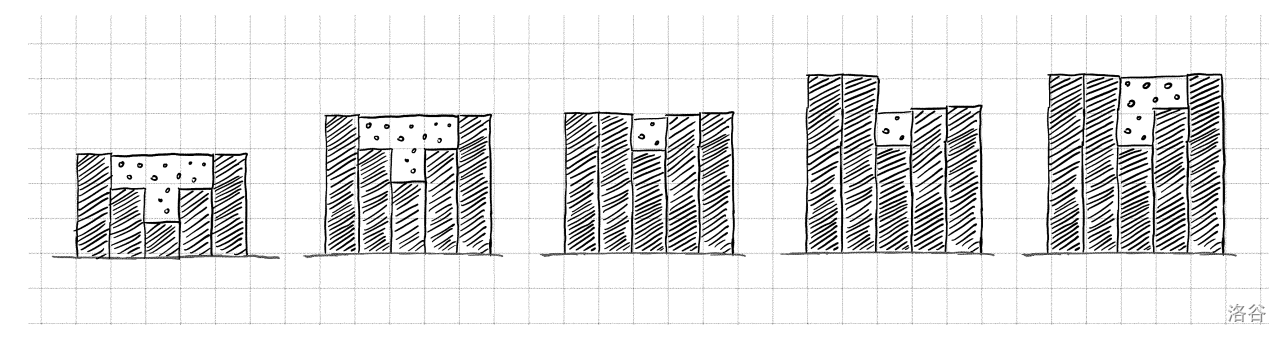
One of the streets in Saint Petersburg has an unusual shape --- it is a narrow stripe of $n$ sections $1$ meter long each, where section $i$ is at the height $a_i$ meters from the ground. The stripe is $1$ meter deep and bounded on the front and on the back by incredibly high buildings. Because of this, when it is raining, a certain amount of rain will accumulate, unable to flow out of the street from either its leftmost or rightmost end. Given the heights $a_1, a_2, \ldots, a_n$, you need to determine the amount of rain (in cubic meters) which will accumulate on the street.

Moreover, your colleagues from the metropolitan construction company will be visiting for $q$ days and on day $i$ they will be laying asphalt on all sections from $l_i$ to $r_i$ inclusive, thus increasing the height of each section $l_i, l_i+1, \ldots, r_i$ by $1$ meter. You need to determine the total amount of water which accumulates on the street before the construction works, and also after every single day of the construction works.

输入格式

The first line contains the number of blocks $n$ and the number of construction events $q$ ($1 \le n, q \le 2 \cdot 10^5$). The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 10^9$) --- the height of each section before all the events. Each of the following $q$ lines contains a pair of integers $l_i$, $r_i$ ($1 \le l_i \le r_i \le n$), denoting the construction work from $l_i$ to $r_i$ inclusive.

输出格式

Print $q+1$ integers --- the amount of water on the street before all updates, and also after every update.

5 4
3 2 1 2 3
1 5
2 4
1 2
5 5

4
4
1
1
3

7 3
1 1000000000 1 1 1 1000000000 1
1 3
4 5
5 7

2999999997
2999999996
2999999994
2999999996

提示

The picture illustrates the amount of water accumulating on the street in the first example.