题目描述

The city of F. can be represented as a tree. A famous fugitive is hiding in it, and today a faithful police officer decided to catch him at all costs. The police officer is stronger than the fugitive, but the fugitive is much faster than the former. That is why the pursuit proceeds as follows. At the moment $t = 0$ the police officer appears at the vertex with number $s$, and the fugitive spawns at any other vertex of his choice. After that, they take turns, starting with the police officer.

• During the police officer's move, she selects any vertex adjacent to the one where she is currently located and moves there. The police officer spends one minute moving. Also, the police officer may decide to stand still instead, in which case she waits one minute at the vertex at which she started her move. If at the end of the turn the police officer ends up at the same vertex as the fugitive, she instantly catches him and the chase ends.
• The fugitive's move is as follows. Let him be at vertex $b$, and the police officer at vertex $p$. Then the fugitive chooses any vertex $b' \ne p$ such that the path between the vertices $b$ and $b'$ does not contain vertex $p$ and instantly moves there. In particular, he can always choose $b' = b$ to stay where he is. The fugitive's move takes no time.

输入格式

The first line contains an integer $n$ — the number of vertices in the tree ( $2 \le n \le 100$ ). The next $n - 1$ lines describe the city of F.: each of them contains a pair of integers $u_i$ , $v_i$ — the numbers of the ends of an edge ( $1 \le u_i, v_i \le n$ ). These edges are guaranteed to form a tree.

The last line contains an integer $s$ — the number of the vertex where the police officer initially appears ( $1 \le s \le n$ ).

输出格式

Print one real number — the mathematical expectation of the duration of the chase with the optimal strategies of the police officer and the fugitive. Your answer will be accepted if its absolute or relative error does not exceed $10^{-6}$ ; formally, if $p$ is your answer, and $j$ is the jury's answer, this should hold: $\frac{|p - j|}{\max\{1, |j|\}} \le 10^{-6}$ .

2
1 2
2

1

3
1 2
1 3
1

2

4
4 3
4 1
4 2
4

3.66667

7
1 4
4 5
5 2
4 6
6 7
7 3
3

8.3525

提示

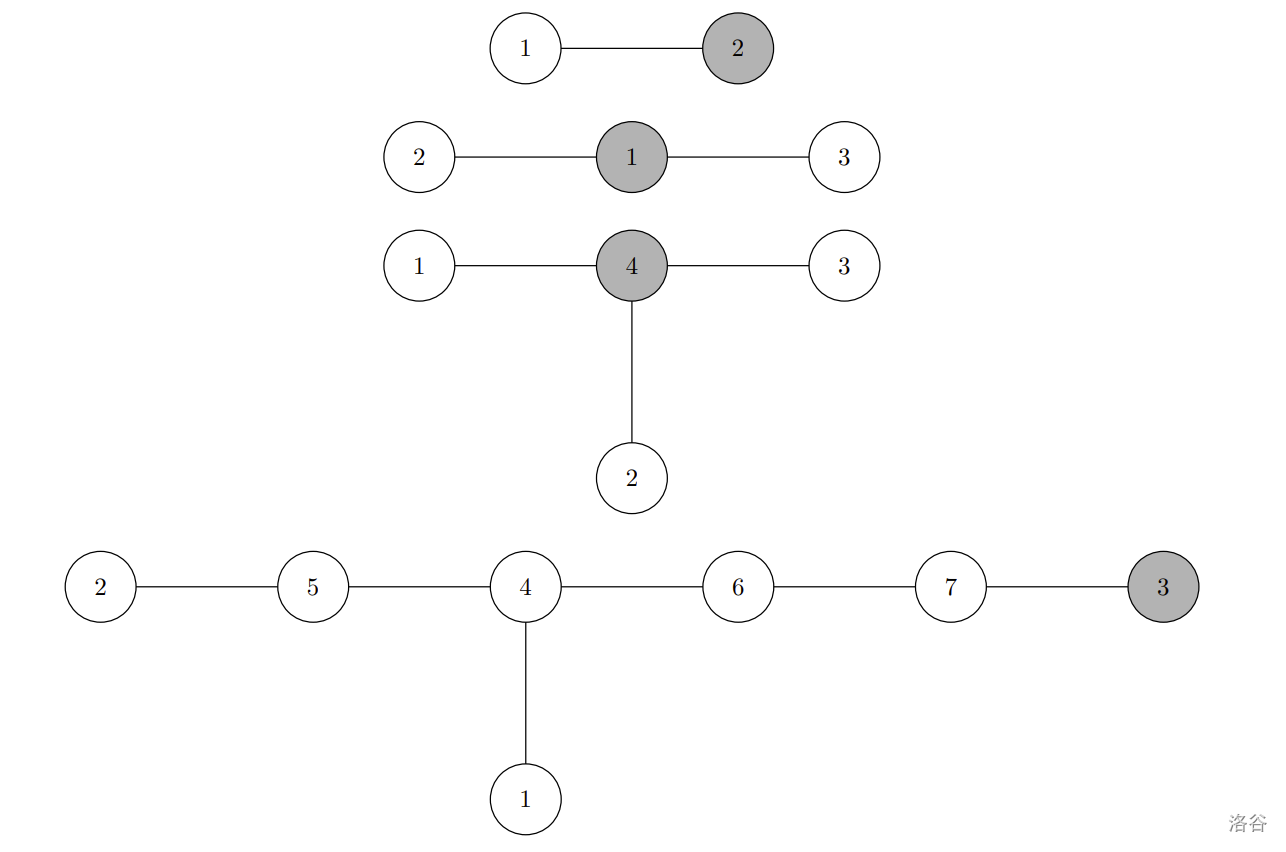
The trees from the examples are depicted below.