题目描述

You are in charge of developing new properties in the suburbs of Toruń. You have already decided that there will be one main street and $n$ properties numbered from 1 to $n$ along the street. The area is somewhat hilly, and the elevation of the $i$-th property is $a_i$ centimetres.

It turns out that no one wants to buy a property that is on a slope. Formally, for elevations $a_1, a_2, \ldots, a_n$, a slope is a contiguous subsequence $a_{i-1}, a_i, \ldots, a_j, a_{j+1}$ with $2 \leq i \leq j \leq n-1$ such that either (i) $a_{i-1} < a_i = a_{i+1} = \ldots = a_j < a_{j+1}$, or (ii) $a_{i-1} > a_i = a_{i+1} = \ldots = a_j > a_{j+1}$. Intuitively, a slope is a contiguous range of properties at positions $i-1, i, i+1, \ldots, j, j+1$, where the elevations of all properties at positions $i, i+1, \ldots, j$ are equal to some $h$, and $h$ is strictly between $a_{i-1}$ and $a_{j+1}$.

You are able to increase or decrease the elevation of any property by any integer, but of course you want to minimise the overall effort. Your task is to determine the minimal total change in elevation such that there are no slopes at all. That is, you want to find elevations $b_1, b_2, \ldots, b_n$ without slopes such that $|a_1 - b_1| + |a_2 - b_2| + \ldots + |a_n - b_n|$ is as small as possible. The elevations $b_i$ must be integers (in particular, they don't have to be positive), and there are no other constraints on $b_i$.

输入格式

The first line contains an integer $n$ ($1 \leq n \leq 2 \cdot 10^5$) denoting the number of properties along the street.

The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($0 \leq a_i \leq 10^9$), where the $i$-th integer $a_i$ is the initial elevation of the $i$-th property.

输出格式

You should output the minimal total change in elevation to ensure that there are no slopes.

11
7 2 1 2 5 7 8 8 10 8 8

5

提示

This is illustrated below. The dashed lines represent the changed elevations without slopes bi of their corresponding properties.

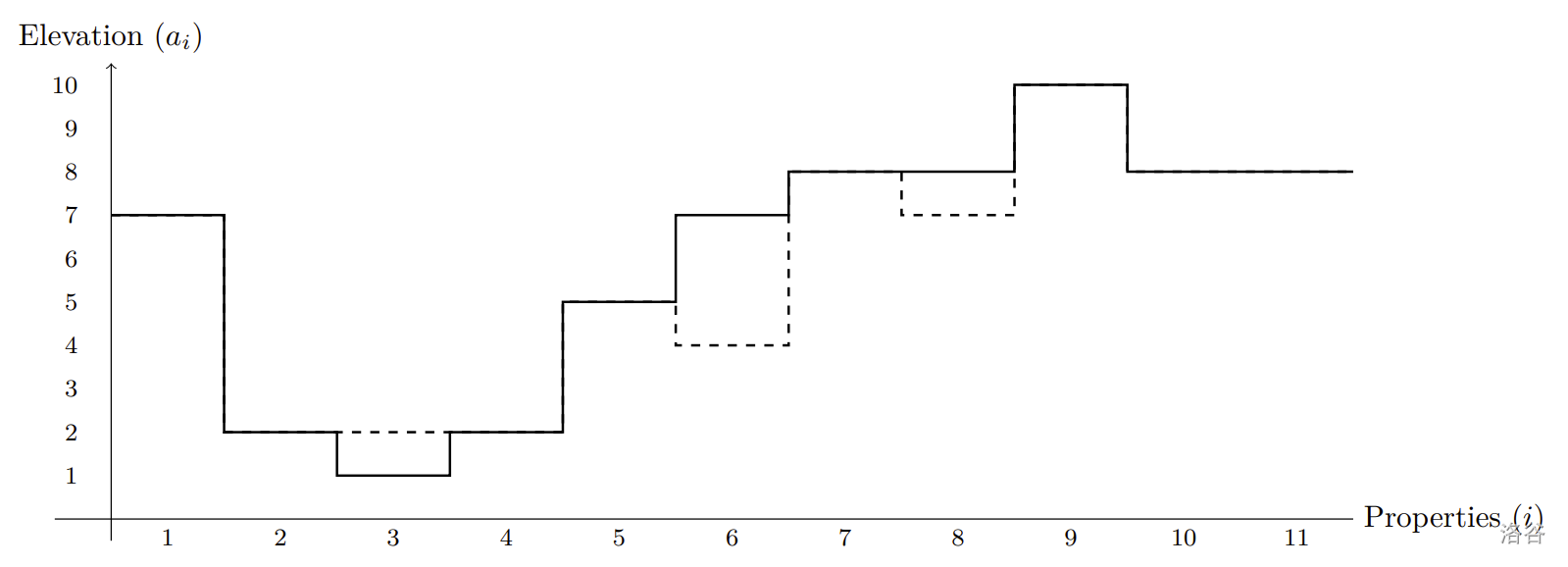
Scoring