#P12428. [BalticOI 2025] Tower
[BalticOI 2025] Tower
题目描述
There are many legends concerning the Leaning Tower of Toruń. The wall of the tower is a circle with evenly spaced doors (in other words, the doors are the vertices of a regular -gon). The doors are numbered from 0 to , but in a random order. Please refer to the scoring section for more details about this.
One of the less known legends describes how every new inhabitant of the tower had to complete a certain challenge. The goal of the challenge was to list the doors, starting with some door and then walking around the circle (clockwise or counterclockwise), visiting each door exactly once.
This needs to be done without actually seeing the tower. Instead, the new inhabitant can ask questions of the following form: "Given three distinct doors , which pairs of doors are the closest to each other: , , or ?". The answer to such a question are all pairs (among , and ) of doors with the smallest Euclidean distance. The distance is simply the length of the shortest segment connecting the doors. Your task is to write a program that will ask a small number of such questions to determine the order of the doors.
Interaction
This is an interactive task. You should write a program which finds a correct solution to the task and communicates with the interactor by reading from the standard input and writing to the standard output.
At the beginning of the interaction, your program should read two integers and (, ) from the standard input, denoting the number of test cases and the maximum allowed average number of queries, respectively. See the scoring section for more information about the latter.
For each test case, your program should first read a single integer () from the standard input, denoting the number of doors in the tower.
Then your program should ask the questions in the following way:
- Your program should write a single line in the form of
to the standard output, where , , and are distinct integers (). This line represents a single question concerning doors , , and . - The response will be given as:
where is an integer () representing the number of pairs of doors with the smallest distance. Each such pair is described by two integers and ( and ).
Once you have determined the order of the doors, you should write a single line in the form of
to the standard output, where is the order of the doors as described in the task statement. Please note that there are exactly possible correct answers since you can output the order starting from any door and then going in either direction. Any of them will be accepted.
Keep in mind that after each query or answer you have to flush the output buffer using cout.flush() (or fflush(stdout) if using printf) in C++ or sys.stdout.flush() in Python. Otherwise your program may receive a Time Limit Exceeded verdict.
After writing the answer to the interactor, your program should immediately proceed to the next test case or end the interaction if all test cases have been processed.
Your program cannot open any files or use any other resources. It can use the standard error stream for debugging purposes, but please mind that writing to this stream takes time.
Please also note that the interactor is not adaptive, meaning that the initial order of the doors is fixed beforehand in each test case and does not change during the interaction.
输入格式
See Interation.
输出格式
See Interation.
提示
Suppose we have only one test case with , and the order of the doors is . The interaction could look as follows:
| Interactor | Your program | Comment |
|---|---|---|
| 1 100 | and . | |
| 6 | Interactor gives the number of doors in the first test case. | |
| ? 0 1 2 | Your program asks which pairs of doors are the closest. | |
| 2 | Pairs of doors and are the closest. | |
| 0 2 | ||
| 1 2 | ||
| ? 4 1 3 | Your program asks which pairs of doors are the closest. | |
| 1 | Pair is the closest. | |
| 1 4 | ||
| ? 0 5 1 | Your program asks which pairs of doors are the closest. | |
| 3 | Pairs , and are the closest. | |
| 0 5 | ||
| 0 1 | ||
| 1 5 | ||
| ! 4 5 3 0 2 1 | Your program correctly outputs the order of the doors. |
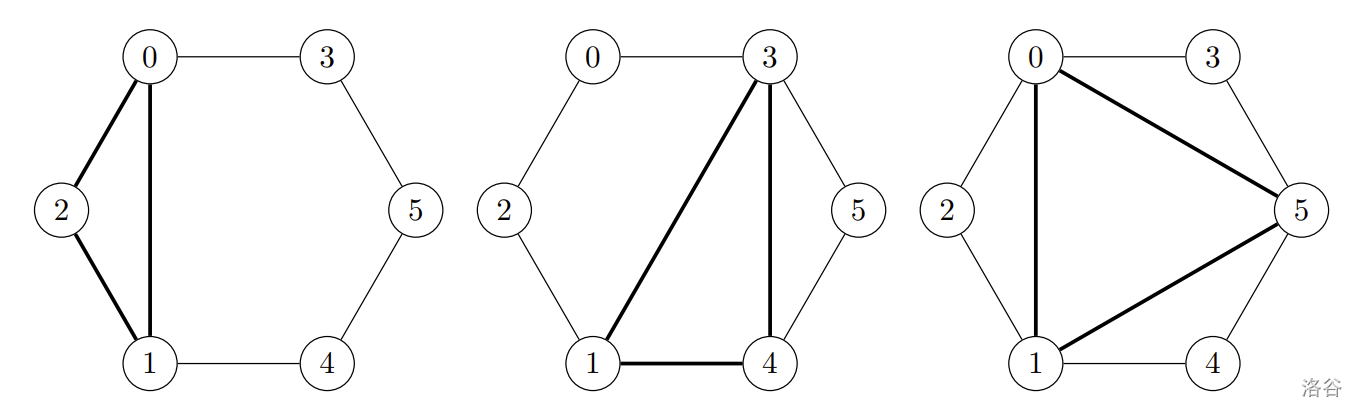
Explanation of the example: The pictures above show the doors with their numbers along the walls of the tower. In the first picture from the left a triangle formed by the doors with numbers is shown, corresponding to the first query of your program. We can see that the pairs and are the closest. In the middle picture a triangle formed by the doors with numbers is shown, corresponding to the second query of your program. We can clearly see that the pair is the closest. In the third picture from the left a triangle formed by the doors with numbers is shown, corresponding to the third query of your program. We can clearly see that all the pairs of doors are equally close to each other.
Please note that the sequences or (and a couple others) would also be correct answers in this case.
Scoring
Scoring for this problem is divided into subtasks. For each subtask there is exactly one test and this single test contains exactly test cases. For each test, the average number of queries asked by your program is calculated by taking the total number of queries among all test cases and dividing it by the number of test cases. If this average is greater than for a given subtask, you will receive a score of for that subtask. Otherwise, for subtasks to , you will receive full score for that subtask.
For the last subtask, your score will be calculated as follows. Let be the actual average number of queries asked by your program. Then, the number of points is given by the following formula:
$$\left\lceil 56 \cdot \min \left(1, \frac{12000 - k^*}{7800}\right) \right\rceil$$meaning that your score increases linearly from to as goes from to .
Please note that if your program gives an incorrect answer to any test case, you will receive a score of for that subtask regardless of the number of queries asked.
The additional constraints for each subtask are in the table below.
| Subtask | Constraints | Points |
|---|---|---|
| 1 | 6 | |
| 2 | 7 | |
| 3 | 9 | |
| 4 | , there is a correct answer where for | 22 |
| 5 | up to 56 |
Moreover, you can assume that each test case has been generated by first choosing uniformly at random from all values of satisfying the constraints of a given subtask, and then choosing the order of the doors uniformly at random from all orders of doors satisfying the constraints of a given subtask.
