题目描述

蜂巢由大量的六边形拼接而成，定义蜂巢中的方向为：$0$ 表示正西方向，$1$ 表示西偏北 $60^\circ$，$2$ 表示东偏北 $60^\circ$，$3$ 表示正东，$4$ 表示东偏南 $60^\circ$，$5$ 表示西偏南 $60^\circ$。

对于给定的一点 $O$，我们以 $O$ 为原点定义坐标系，如果一个点 $A$ 由 $O$ 点先向 $d$ 方向走 $p$ 步再向 $(d+2) \bmod 6$ 方向（$d$ 的顺时针 $120^\circ$ 方向）走 $q$ 步到达，则这个点的坐标定义为 $(d, p, q)$。在蜂窝中，一个点的坐标可能有多种。

下图给出了点 $B(0, 5, 3)$ 和点 $C(2, 3, 2)$ 的示意。

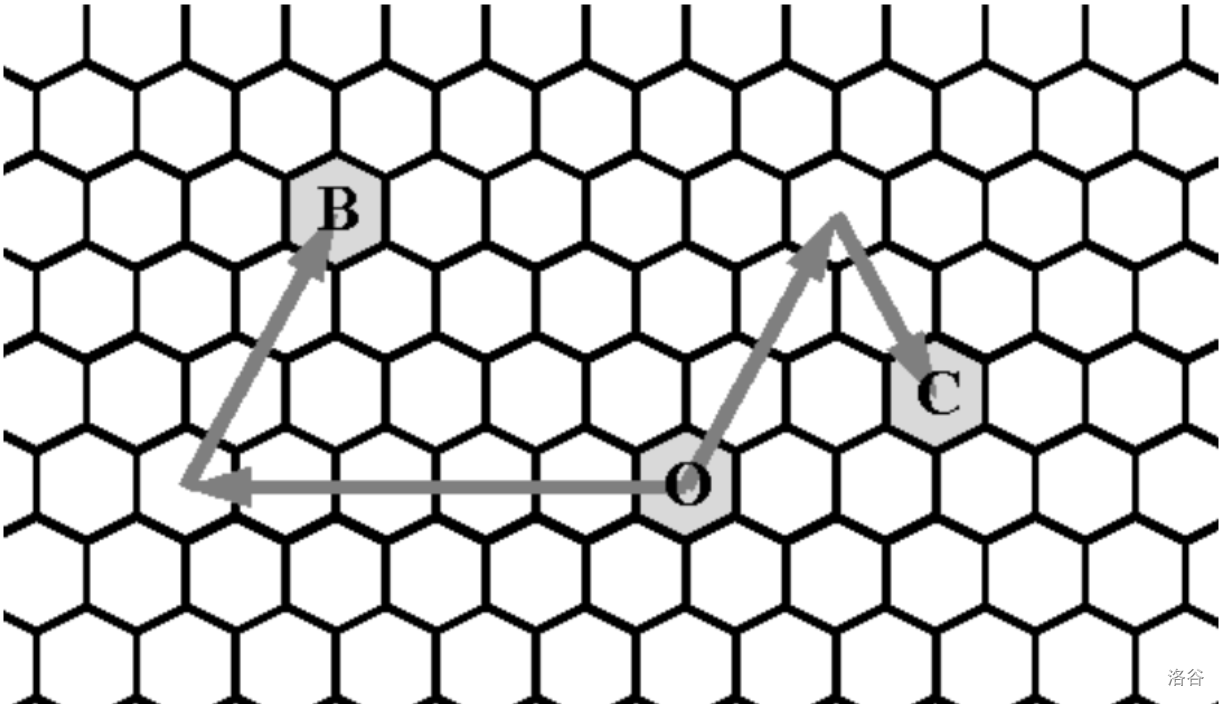
给定点 $(d_1, p_1, q_1)$ 和点 $(d_2, p_2, q_2)$, 请问他们之间最少走多少步可以到达?

输入格式

输入一行包含 $6$ 个整数 $d_1, p_1, q_1, d_2, p_2, q_2$ 表示两个点的坐标, 相邻两个整数之间使用一个空格分隔。

输出格式

输出一行包含一个整数表示两点之间最少走多少步可以到达。

0 5 3 2 3 2

7

提示

评测用例规模与约定

• 对于 $25\%$ 的评测用例, $p_1, p_2 \leq 10^3$;
• 对于 $50\%$ 的评测用例, $p_1, p_2 \leq 10^5$;
• 对于 $75\%$ 的评测用例, $p_1, p_2 \leq 10^7$;
• 对于所有评测用例, $0 \leq d_1, d_2 \leq 5$, $0 \leq q_1 < p_1 \leq 10^9$, $0 \leq q_2 < p_2 \leq 10^9$。