题目背景

版权信息：译自 2025年度 国际情报 올림피아드 (Olympiad) 代表学生 选拔考试 R1T4。[CC BY-NC-SA 4.0]

题目描述

平面上有 $n$ 个矩形。第 $i$ 个矩形包含的点为 $\{(x,y):x\in [A_i,C_i], y\in [B_i,D_i]\}$。（点在矩形边界上，或者在矩形内部，都算包含。）

定义两个矩形相连，当且仅当存在一个点被这两个矩形同时包含。

定义两个矩形 $a,b$ 连通，当且仅当存在一个长度为 $k$（$k\ge 1$）的序列 $s_1,s_2,\ldots,s_k$（$s_1=a,s_k=b$），满足 $\forall 1\le i\lt k$，都有 $s_i$ 与 $s_{i+1}$ 相连。

定义矩形集合 $S$ 为连通分量，当且仅当：

• $\forall i,j\in S$，都有 $i,j$ 连通；
• $\forall i\in S,j\not\in S$，都有 $i,j$ 不连通。

给定这 $n$ 个矩形的信息，求出所有的连通分量。

实现细节

你不需要，也不应该实现 main 函数。你的程序禁止使用 stdin / stdout。

你应该实现以下的函数：

vector<int> find_union(int n, vector<int> A, vector<int> B, vector<int> C,
vector<int> D);

• $n$：矩形的个数；
• $A,B,C,D$：长度为 $n$ 的整数数组，第 $i$ 个矩形包含的点为 $\{(x,y):x\in [A[i-1],C[i-1]], y\in [B[i-1],D[i-1]]\}$。
• 令连通分量的个数为 $m$。你需要返回一个长度为 $n$，值域为 $[0,m)$ 的非负整数数组 $u$，满足 $u_i=u_j\iff i,j$ 在一个连通分量内。

输入格式

Sample Grader 输入格式如下：

第一行，正整数 $n$。

接下来 $n$ 行，第 $i$ 行四个整数 $A_{i},B_{i},C_{i},D_{i}$。

输出格式

Sample Grader 输出格式如下：

输出 $n$ 个非负整数 $u_0,u_1,\ldots,u_{n-1}$。

3
0 0 1 1
1 1 2 2
2 -1 4 0

0 0 1

2
0 1 3 3
2 0 4 2

0 0

提示

样例交互

样例交互 $1$

样例 $1$ 中，$n = 3, A = [0, 1, 2], B = [0, 1, −1], C = [1, 2, 4], D = [1, 2, 0]$。

交互库调用

find_union(3, {0, 1, 2}, {0, 1, -1}, {1, 2, 4}, {1, 2, 0});

对应的矩形如图所示。

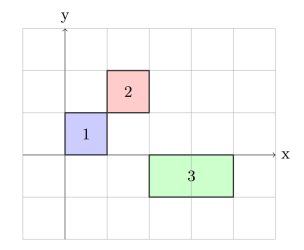
由于 $(1,1)$ 同时被矩形 $1,2$ 包含，所以矩形 $1,2$ 连通。

返回 $[0,0,1]$。返回 $[1,1,0]$ 也是正确的。

样例交互 $2$

样例 $2$ 中，$n = 2, A = [0, 2], B = [1, 0], C = [3, 4], D = [3, 2]$。

交互库调用

find_union(2, {0, 2}, {1, 0}, {3, 4}, {3, 2});

对应的矩形如图所示。

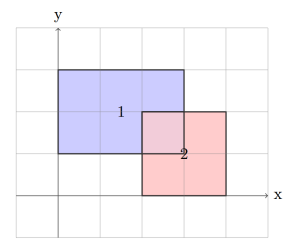
显然只有唯一的一个返回值 $[0,0]$。

数据范围

• $1\le n\le 5\times 10^5$；
• $-10^9\le A_i,B_i,C_i,D_i\le 10^9$；
• $A_i\le C_i$；$B_i\le D_i$。

子任务

• $\text{Subtask 0 (0 pts)}$：样例。
• $\text{Subtask 1 (3 pts)}$：$\forall 0\le i\le n-1$，$A[i] \le i \le C[i], B[i] \le 0 \le D[i]$。
• $\text{Subtask 2 (4 pts)}$：$\forall 0\le i\le n-1$，$B[i] \le 0 \le D[i]$。
• $\text{Subtask 3 (7 pts)}$：$n\le 5\times 10^3$。
• $\text{Subtask 4 (21 pts)}$：$A_i=C_i$ 或 $B_i=D_i$ 至少有一个成立。
• $\text{Subtask 5 (26 pts)}$：$n\le 10^5$。
• $\text{Subtask 6 (39 pts)}$：无额外约束。