题目描述

彼得是一位生物學家。有次他在兩筆資料中分析同一群現存物種集合 $\Sigma = \{1, 2, \ldots, n\}$ 間的演化關係，卻得到了不太一樣的演化樹，想知道這兩棵演化樹的類似程度。

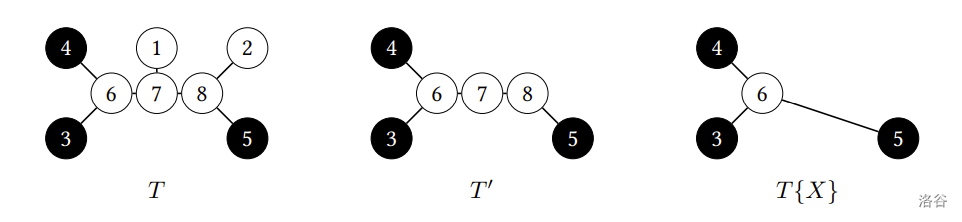
一棵演化樹 $T$ 是一棵無向無根樹 (undirected, unrooted tree)，其中葉節點為現存物種 $1, 2, \ldots, n$，其他節點則為已滅絕物種。設 $v \in V(T)$，我們用 $\deg(v)$ 來表示與節點 $v$ 相鄰的節點個數。在一棵演化樹中，每個代表已滅絕物種的節點 $v$ 均有 $\deg(v) \ge 3$。對於一個現存物種的子集合 $X \subseteq \Sigma$，我們用 $T\{X\}$ 來代表 $X$ 中的現存物種在 $T$ 上的演化關係所形成的「演化子樹」，建構方式如下：

1. 對所有 $X$ 中的任兩點，標記其在 $T$ 上的簡單路徑，並將所有不在 $X$ 且未被標記的點刪除以得到 $T'$。
2. 從 $T'$ 中不斷刪除滿足 $\deg(v) = 2$ 的非葉節點 $v$ 以得到 $T\{X\}$：將與 $v$ 連結的兩條邊合併成一條，並移除 $v$。

以下圖的演化樹 $T$ 為例。$T$ 裡的現存物種集合為 $\Sigma = \{1, 2, 3, 4, 5\}$，若取 $X = \{3, 4, 5\}$，則經步驟 $1$ 後會得到 $T'$，再經過步驟 $2$ 後會得到 $T\{X\}$。注意當 $X = \emptyset$ 時，根據定義我們有 $T\{X\} = \emptyset$。

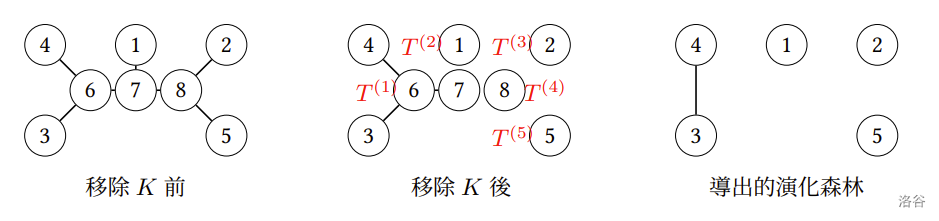
從一棵演化樹 $T$ 中移除大小為 $k \ge 0$ 的任意邊集合 $K$，可以得到 $k+1$ 棵子樹 $T^{(1)}, T^{(2)}, \ldots, T^{(k+1)}$，其中每棵子樹 $T^{(i)}$ 上的物種在 $T$ 中的演化關係都會構成一棵演化子樹，我們稱它們為從 $T$ 中移除 $K$ 所導出的演化森林。注意我們有

1. $T$ 自身為移除 $\emptyset$ 後導出的演化森林。
2. 若一棵子樹 $T^{(i)}$ 上沒有任何現存物種，對應的演化子樹為空。

以上圖中的 $T$ 為例，移除 $K = \{(1, 7), (7, 8), (2, 8), (5, 8)\}$ 四條邊可以得到五棵子樹 $T^{(1)}, T^{(2)}, \ldots, T^{(5)}$，接著導出演化森林：

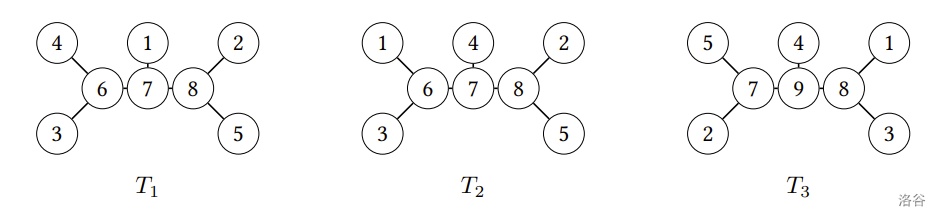
比較兩座現存物種相同的演化森林時，我們只關注現存物種間的關係，因此已滅絕物種（即非葉節點）的編號並不重要。設 $F_1$ 與 $F_2$ 為兩座現存物種相同的演化森林，若移除它們的非葉節點編號後變得完全相同，我們就稱 $F_1$ 與 $F_2$ 類似。更精確地說，我們稱 $F_1$ 與 $F_2$ 類似，若且唯若存在某個一對一函數 $\Phi: V(F_1) \to V(F_2)$，滿足

1. 對任意 $u \in \Sigma = \{1, 2, \ldots, n\}$，我們有 $\Phi(u) = u$。
2. 對任意 $u, v \in V(F_1)$，我們有

$$(u, v) \in E(F_1) \iff (\Phi(u), \Phi(v)) \in E(F_2). $$

以下圖為例，如果將 $T_1, T_2, T_3$ 的非葉節點編號都移除，會發現 $T_1$ 與 $T_2$ 不類似，而 $T_2$ 與 $T_3$ 類似。

設 $T_1$ 與 $T_2$ 為現存物種相同的兩棵演化樹。若存在從 $T_1$ 與 $T_2$ 中各刪除 $k$ 條邊的方法，使得兩者導出的演化森林類似，則稱 $T_1$ 與 $T_2$ 的差異不大於 $k$，而滿足此條件的最小整數 $k^*$ 稱為 $T_1$ 與 $T_2$ 的差異數。如上圖中 $T_2$ 與 $T_3$ 的差異數為 $0$，而 $T_1$ 與 $T_2$ 的差異數為 $1$。

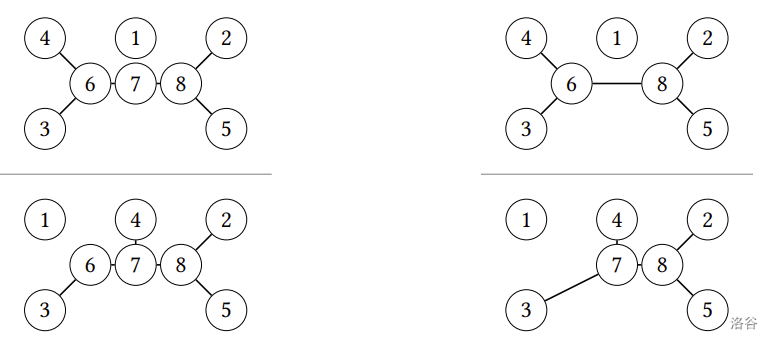
從 $T_1$ 與 $T_2$ 各刪除 $1$ 條邊 | 導出了類似的演化森林

設從 $T_1$ 與 $T_2$ 中刪除的邊集合分別為 $K_1$ 與 $K_2$，兩種刪除方法被視為不同若且唯若 $K_1$ 不同或 $K_2$ 不同。現給定兩棵物種集合均為 $\Sigma$ 的演化樹 $T_1, T_2$ 以及一個整數上限 $k$，彼得想知道它們的差異數 $k^*$ 是否不大於 $k$；如果 $1 \le k^* \le k$，彼得也想知道有多少種從 $T_1$ 和 $T_2$ 中各刪除 $k^*$ 條邊的方法，可以使它們導出類似的演化森林。

输入格式

$n$ $m_1$ $m_2$ $k$
$u_1$ $v_1$
$u_2$ $v_2$
$\vdots$
$u_{n+m_1-1}$ $v_{n+m_1-1}$
$u_1'$ $v_1'$
$u_2'$ $v_2'$
$\vdots$
$u_{n+m_2-1}'$ $v_{n+m_2-1}'$

• $n$ 代表現存物種集合 $\Sigma = \{1, 2, \ldots, n\}$ 的大小。
• $m_1$ 代表在 $T_1$ 中已滅絕物種（以 $n+1, n+2, \ldots, n+m_1$ 表示）的數量。
• $m_2$ 代表在 $T_2$ 中已滅絕物種（以 $n+1, n+2, \ldots, n+m_2$ 表示）的數量。
• $k$ 代表彼得設定的上限。
• $u_i, v_i$ 代表 $T_1$ 有一條邊從 $u_i$ 連接到 $v_i$。
• $u_i', v_i'$ 代表 $T_2$ 有一條邊從 $u_i'$ 連接到 $v_i'$。

输出格式

如果 $k^* = 0$，請輸出

$0$

如果 $1 \le k^* \le k$，請輸出

$k^*$
$S$

其中 $S$ 為一整數，代表從 $T_1$ 與 $T_2$ 中各刪除 $k^*$ 條邊後導出的演化森林類似的刪除方法數。如果 $k^* > k$，請輸出

$-1$

5 3 3 2
1 7
2 8
3 6
4 6
5 8
6 7
7 8
1 6
2 8
3 6
4 7
5 8
6 7
7 8

1
4

4 2 2 0
1 5
2 5
3 6
4 6
5 6
1 6
2 6
3 5
4 5
5 6

0

6 3 3 2
1 7
2 7
3 7
4 8
5 9
6 9
7 8
8 9
1 7
2 7
3 9
4 9
5 8
6 8
7 8
8 9

2
9

6 1 4 2
1 7
2 7
3 7
4 7
5 7
6 7
1 7
2 7
3 8
4 8
5 9
6 9
7 10
8 10
9 10

-1

提示

測資限制

• $n \ge 2$。
• $0 \le m_1 \le 300-n$。
• $0 \le m_2 \le 300-n$。
• $k \in \{0, 1, 2\}$。
• $1 \le u_i \le n+m_1$。
• $1 \le v_i \le n+m_1$。
• $1 \le u_i' \le n+m_2$。
• $1 \le v_i' \le n+m_2$。
• 給定的 $T_1$ 與 $T_2$ 保證連通，且
  1. 若 $u \in \{1, 2, \ldots, n\}$，則在 $T_1$ 與 $T_2$ 中 $\deg(u) = 1$。
  2. 若 $u \in \{n+1, n+2, \ldots, n+m_1\}$，則在 $T_1$ 中 $\deg(u) \ge 3$。
  3. 若 $u \in \{n+1, n+2, \ldots, n+m_2\}$，則在 $T_2$ 中 $\deg(u) \ge 3$。
• 輸入的數皆為整數。

評分說明

本題共有四組子任務，條件限制如下所示。 每一組可有一或多筆測試資料，該組所有測試資料皆需答對才會獲得該組分數。

子任務	分數	額外輸入限制
1	$21$	$k = 0$
2	$13$	$k \in \{0, 1\}$
3	$23$	$n+m_1 \le 30$ 且 $n+m_2 \le 30$
4	$43$	無額外限制