#P11869. [威海市赛2024] 状态图
[威海市赛2024] 状态图
题目描述
小威在数电课上学到了状态转换图,比如下面这张:
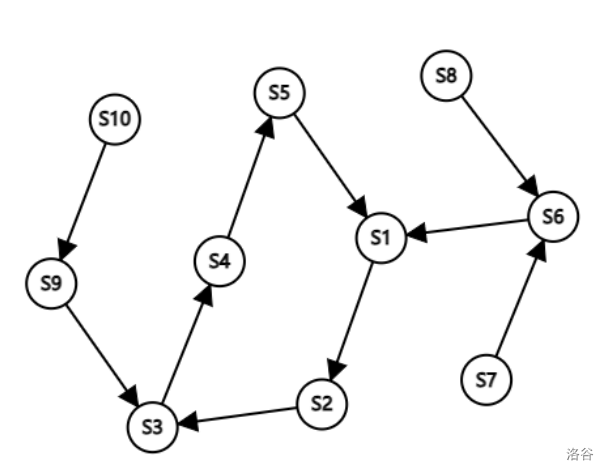
现在,他遇到了一个同步时序电路分析的问题,其状态转换图有一定的特点:
假设总共有 个节点,分别为 。
当时钟信号下一个脉冲为"高(1)"时,节点 转移到节点 ;
当时钟信号下一个脉冲为"低(0)"时,节点 转移到节点 。
而在本题中,时钟信号的脉冲序列为 101010....
现在小威想知道,对于给定的 ,是否存在一个时钟周期 ,使得从任意节点 任意时刻(即初始脉冲可能为 0,也可能为 1)出发都能在 个脉冲之后回到初始状态(状态包括节点和脉冲两个方面,两状态相同当且仅当节点和脉冲都相同),存在则输出最小的时钟周期 ,否则输出 inf。
输入格式
第 1 行一个整数 代表数据组数。
第 2 行到第 行每行五个整数 ,含义如上所述。
对于所有数据,满足:
- ;
- ;
- ;
- 。
输出格式
行,每行一个正整数或字符串表示答案,含义如上所述。
3
5 2 1 3 4
6 2 1 3 5
1732 1233 627 911 1247
8
inf
864
10
3 2 2 2 1
5 2 3 4 2
6 1 3 1 0
5 3 3 2 1
5 4 2 4 1
9 2 5 6 2
6 4 1 1 3
6 1 1 5 1
8 4 7 0 3
9 1 7 3 8
6
10
inf
4
8
18
inf
2
inf
18
提示
样例 #1 解释如下:
对于第一组数据,节点的状态转换序列可以拆分如下(括号中的是脉冲高/低):
$S_0(1) \to S_3(0) \to S_2(1) \to S_2(0) \to S_1(1) \to S_0(0) \to S_4(1) \to S_1(0)(\to S_0(1))$,8 个时刻一循环;
,2 个时刻一循环;
取两个循环周期的最小公倍数 8 即是答案。
对于第二组数据,从 出发,从 0 脉冲对应时刻开始转移,无论如何也无法回到起始状态(除初始时刻外,不存在同时让节点等于 ,脉冲为 0 的时刻)。
