题目描述

给定一棵 $N$ 个点的有根树 $T$，保证根结点的编号为 $1$。

树上的一个点 $s$ 会被选中，距离 $s$ 不超过 $R$ 的点会被感染，两个点的距离定义为其树上路径的边数。

一对点是可达的当且仅当它们都没有被感染，且其树上路径经过被感染的点数不超过 $M$。

对于 $s=1,2,\cdots,N$ 计算选中 $s$ 的可达点对数量。

输入格式

第一行输入三个整数 $N,R,M$。

第二行输入 $N-1$ 个整数 $p_2,p_3,\cdots,p_N$，代表每个点的父亲。

输出格式

输出 $N$ 行，每行一个整数，第 $s$ 行的整数代表选择 $s$ 的答案。

13 2 2
1 2 3 4 3 6 6 8 2 10 11 1

16
4
15
55
66
36
66
55
66
45
55
66
66

3 0 1
1 2

1
1
1

提示

【样例解释】

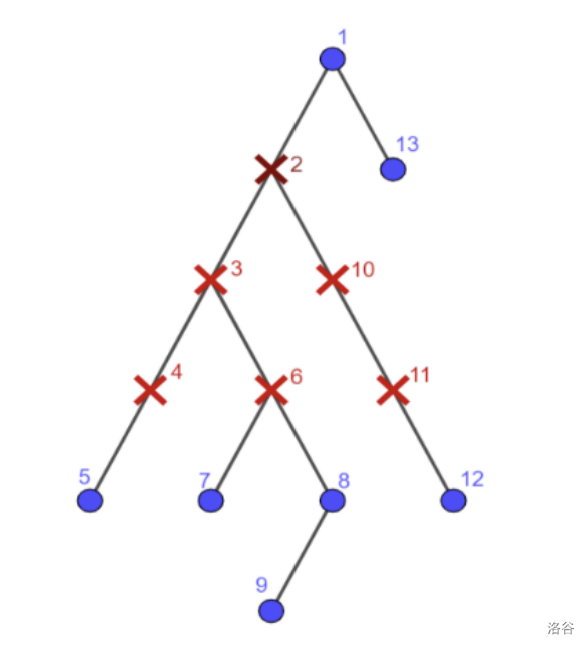
$s=2$ 的树如图所示。

所有可达点对为 $(1,13)$，$(7,8)$，$(7,9)$ 和 $(8,9)$。

注意 $(1,2)$ 不可达，因为 $2$ 已经被感染；$(1,5)$ 不可达，因为路径上有三个被感染的点 $2,3,4$。

【数据范围】

本题采用捆绑测试。

• Subtask 1（20 pts）：$N\leq 300$。
• Subtask 2（14 pts）：$R=0$。
• Subtask 3（15 pts）：$M=2R+1$。
• Subtask 4（10 pts）：$M=2R-1$。
• Subtask 5（16 pts）：$N\leq 5\times 10^3$。
• Subtask 6（25 pts）：无特殊限制。

对于 $100\%$ 的数据，保证 $2\leq N\leq 5\times 10^5$，$1\leq p_i<i$，$0\leq R\leq N-1$，$0\leq M\leq 2R+1$。