题目背景

:::info[洛谷网校 2025/2026 冬春课程介绍]{close} 洛谷网校将在寒假开设一系列课程，从零基础课程到入门级、提高级乃至省选均有开课。现在已经开放报名。部分课程名额有限，报满则不再接受新的学员。

点击对应的课程链接查看课程的具体信息，或者进行报名。

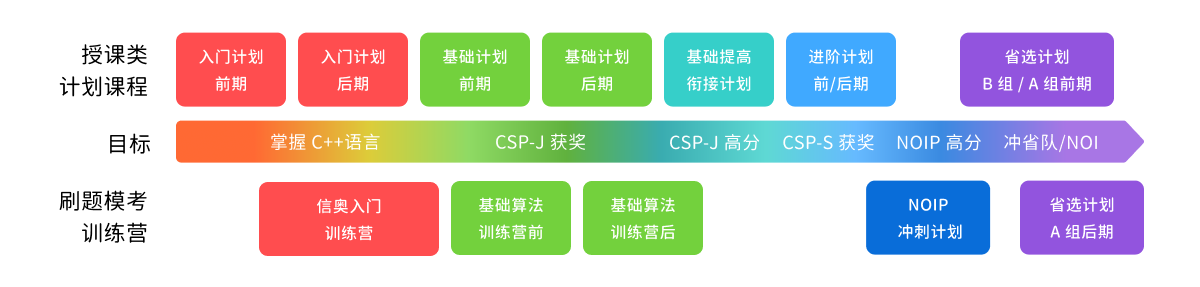
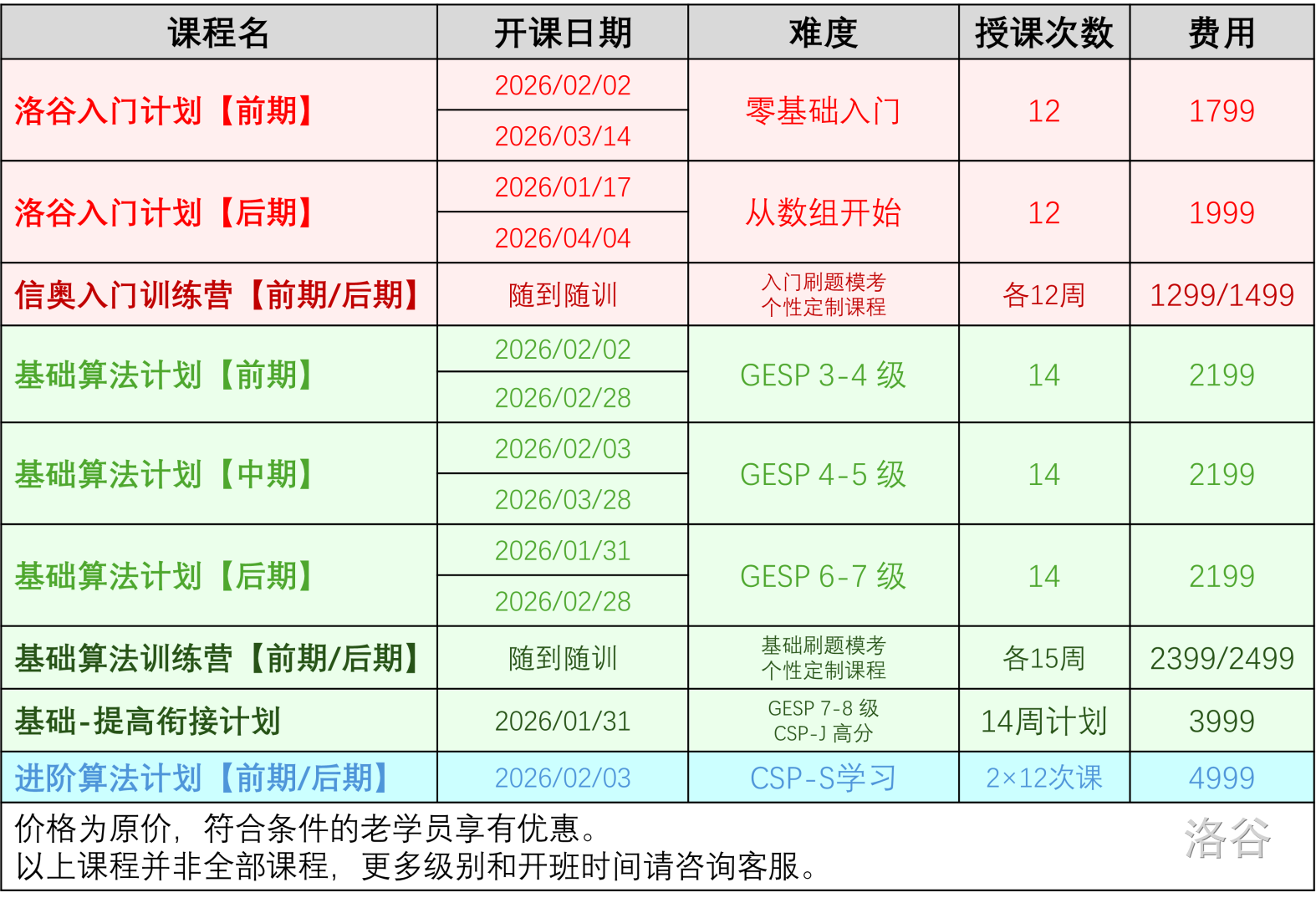
授课课程

各个班级均为 11 月或 2026 年寒假开班，了解详细安排及报名请点击下面的对应的链接。

• 入门前期：从零基础开始学习，内容包括编程软件的安装和使用、顺序结构程序设计、变量与常量、分支结构程序设计、循环结构程序设计，同时包含测试与评估。预期学习完课程后，学员可以达到 CCF GESP 评级一级水平。

  • 二月晚上班（2 月 2 日开课）

• 入门后期：适合已经学习完前期或者其他同类课程的学生。后期课程的内容包括数组、字符串、函数、结构体、文件输入输出等进阶 C++ 语言内容，同时包含测试与评估。初步了解算法竞赛思维，为之后学习算法打下坚实的基础。预期学习完课程后，学员可以达到 CCF GESP 评级二级水平。

  • 一月下午班（1 月 17 日开课）

• 基础前期：已经掌握语言基础。本课程学习内容包括排序、枚举、复杂度分析、二进制、简单数论和组合数学等。辅以针对性的练习，帮助学生搭建算法知识体系。预期学习完课程后，学员可以达到 CCF GESP 评级 3-4 级，CSP-J 获奖水平。

  • 一月晚上班（1 月 10 日开课）
  • 二月上午班（2 月 10 日开课）

• 基础中期：已经学习完前期算法内容。本计划包括简单数据结构（栈/队列/链表/树）、二分、递归、分治、动态规划入门。辅以针对性的练习，加深对基础算法的理解。学员可以达到 CCF GESP 评级 4-5 级，CSP-J 获奖水平。

  • 十一月晚上班（11 月 8 日开课）
  • 二月下午班（2 月 3 日开课）

• 基础后期：已经学习完中期算法内容。本课程学习内容包括搜索、二分、基础动态规划、集合、图等。辅以针对性的练习，进一步完善算法知识体系。预期学习完课程后，学员可以达到 CCF GESP 评级 5-6 级，CSP-J 二等奖水平。

  • 一月下午班（1 月 31 日开班）

欢迎关注洛谷公众号，及时获取更多洛谷相关动态！

点击下方小红书推文，了解信息学竞赛的题目难度区分！

:::

题目描述

洛谷网校共开设 $n$ 类课程，编号依次为 $1, 2, \cdots, n$。学员按照课程 $1, 2, \cdots, n$ 的顺序学完课程，可以在 FCC ION 比赛中取得好成绩。学习讲究循序渐进，在前一个课程学完前，不能开始下一个课程的学习。

小汪决定在接下来的 $m$ 天里在洛谷网校参与学习。接下来的 $m$ 天里，编号为 $i$ 的课程共有 $c_i$ 个班级，第 $j$ 个班级从第 $s_{i,j}$ 天开始，第 $t_{i,j}$ 天结束。

小汪需要从课程 $1$ 开始学习。且在任意一天，小汪只能属于一个班级。也就是说，假设小汪参加的课程 $3$ 的班级在第 $20$ 天结束，且有课程 $4$ 的一个班级在第 $20$ 天开始，小汪无法参加课程 $4$ 的这个班级。

现在，给出洛谷网校的开课计划，请问小汪最早在第多少天结束全部课程的学习。如果无法在 $m$ 天内学完，请输出 $-1$。

输入格式

第一行两个整数 $n,m$。

接下来 $n$ 行，第 $i$ 行描述课程 $i$ 的情况：

• 第一个整数为 $c_i$，表示班级的数目。
• 接下来 $2\cdot c_i$ 个整数，每两个整数描述一个班级，分别为 $s_{i,j}$ 与 $t_{i,j}$。

输出格式

输出一行一个整数，表示答案。

4 20
4 1 3 5 7 9 11 16 18
4 2 4 6 7 7 9 11 16
4 4 5 7 8 10 11 17 18
4 2 4 6 8 13 15 18 19

15

4 15
2 1 2 10 12
1 11 14
1 15 15
1 15 15

-1

提示

【样例 1 解释】

开班和学习情况如下图所示。黄色表示小汪所参加的班级。

【样例 2 解释】

在 $15$ 天内最多上完课程 $3$，无法完成课程 $4$。

【数据规模与约定】

对于 $30\%$ 的测试数据，$c_i=1$。

对于 $70\%$ 的测试数据，$1 \le n \le 30$，$1 \le s_{i, j} \le t_{i, j} \le m \le 10^5$，$1 \le c_i \le m$。

对于 $100\%$ 的测试数据，$1 \le n \le 10^5$，$1 \le s_{i, j} \le t_{i, j} \le m \le 10^9$，$1 \le c_i \le m$，$\sum c_i \le 10^5$。不保证对于任意的 $u<v$，$s_{i,u}\le s_{i,v}$，不保证对于任意的 $u<v$，$t_{i,u}\le t_{i,v}$。